机器学习概论

作者: 引线小白-本文永久链接：httpss://www.limoncc.com/post/72a5edcac04cd1a3e93a37ee90ac9259/
知识共享许可协议: 本博客采用署名-非商业-禁止演绎4.0国际许可证

一、机器学习若干符号解释

我们在表达概念时，通常用集合论，空间之类的术。这个时候，我们注意元素和集合的区别。而在我们表达运算时，我们通常用矩阵的概念，这个时候你要注意维度、列、行的概念。多加练习，你很快就会掌握这个表达。

1、输入空间

用矩阵表示数据集$\mathcal{D}:\mathit{X}=\left[\begin{array}{c}{\mathit{x}}_1^{\text{T}}\\ {\mathit{x}}_2^{\text{T}}\\ ⋮\\ {\mathit{x}}_n^{\text{T}}\end{array}\right]=\left[\begin{array}{c}{\mathit{x}}_{1,:}^{\text{T}}\\ {\mathit{x}}_{2,:}^{\text{T}}\\ ⋮\\ {\mathit{x}}_{n,:}^{\text{T}}\end{array}\right]=\left[\begin{array}{ccc}{x}_{1,1}& \dots & x_{1,k}\\ ⋮& \dots & ⋮\\ x_{n,1}& \dots & x_{n,k}\end{array}\right]$。${\displaystyle {\mathit{x}}_i={\mathit{x}}_{i,:}}$表示用 ${\displaystyle \mathit{X}}$的第i行转置构造向量 ${\displaystyle \underset{k\times 1}{\underbrace{{\mathit{x}}_i}}}$
用matlab举个例子：

%矩阵与机器学习
>> X=[12, 14, 15; 1.5, 5.4 ,6.7;20,3.4,5]
X =
   12.0000   14.0000   15.0000
    1.5000    5.4000    6.7000
   20.0000    3.4000    5.0000
>> x1=X(1,:)'
x1 =
    12
    14
    15
>> x1(2,1)
ans =
    14

所以 ${\displaystyle {\mathit{x}}_{\mathbf{1}}}$表示包含k个维度的一次观测(示例)。我们用集合论的方式再叙述一遍有n个样本的数据集或者样本空间 ${\displaystyle X=\{{\mathit{x}}_1,{\mathit{x}}_2,\dots ,{\mathit{x}}_i,\dots ,{\mathit{x}}_n\}\subseteq {\mathcal{X}}^n}$ ,其中 ${\displaystyle {\mathit{x}}_i}$是样本点(样本)，我们把输入的所有可能取值集合 ${\displaystyle \mathcal{X}}$叫做输入空间,无监督学习下也可以称为样本空间。显然 ${\displaystyle X\subseteq {\mathcal{X}}^n}$。

输入空间的矩阵表示和集合表示我们需要多加熟悉、灵活运用。这是我们思考多维问题的基础。

2、输出空间

集合${\displaystyle Y=\{y_1,y_2,..,y_i,\dots ,y_n\}\subseteq \mathcal{Y}}$，其中输出空间 ${\displaystyle \mathcal{Y}}$、 输入样本${\displaystyle Y}$、输入样本点 ${\displaystyle y_i}$。

矩阵表示： ${\displaystyle \mathit{y}=[y_1,y_2,..,y_i,\dots ,y_n{]}^{\text{T}}}$

在有监督学习中，我们把集合 ${\displaystyle \{({\mathit{x}}_i,y_i)\mid 1⩽i⩽n\}}$也叫做训练集$\mathcal{D}$ ，${\displaystyle ({\mathit{x}}_i,y_i)}$表示第i个样本。

符号${\displaystyle P(y\mid \mathit{x})=\mathcal{N}(y\mid {\mathit{x}}^{\text{T}}\mathit{\beta },\sigma )}$与${\displaystyle y\mid \mathit{x}\sim \mathcal{N}({\mathit{x}}^{\text{T}}\mathit{\beta },\sigma )}$是同一个意思。注意 ${\displaystyle \mid }$的不同意思。[^1]

统计学中，我们写成这样 ${\displaystyle P(y\mid \mathit{x},\mathit{\beta })}$和 ${\displaystyle P(\mathit{x}\mid \mathit{\beta })}$

机器学习中，我们写成这样 ${\displaystyle P(y\mid \mathit{x},\mathit{w})}$和 ${\displaystyle P(\mathit{x}\mid \mathit{w})}$

3、假设空间：

1、如果真实的世界的关系是 ${\displaystyle y=h(\mathit{x})}$， 世界充满噪声。所以 ${\displaystyle y=h(\mathit{x})+e}$。

现在我们有一个样本或者数据集 ${\displaystyle \mathcal{D}=\{({\mathit{x}}_i,y_i){\}}_{i=1}^n}$。我们想通过这个数据集 ${\displaystyle \mathcal{D}}$估计出 ${\displaystyle f(\mathit{x})}$来找到 ${\displaystyle h(\mathit{x})}$。其实我们能找到的 ${\displaystyle f}$有很多，现在我们把它汇集起来： ${\displaystyle \mathcal{H}=\{f_i\}}$。我们的模型是 ${\displaystyle y=f(\mathit{x})+\epsilon }$。

现在我们换一个说法:
1、世界是这样的： ${\displaystyle p(y=h(\mathit{x})\mid \mathit{x})}$
2、我们观察到的世界是这样的：${\displaystyle \mathcal{D}=\{({\mathit{x}}_i,y_i){\}}_{i=1}^n}$
3、我们假设世界是这样的： ${\displaystyle p(y=f(\mathit{x}\mathbf{)}\mathbf{\mid }\mathit{x},\mathcal{D},M)}$[^1]，其中 ${\displaystyle M}$是模型(算法)。
于是
${\displaystyle \epsilon =y-f=y-h+h-f=y-h+h-\mathrm{E}[f]+\mathrm{E}[f]-f}$
${\displaystyle \mathrm{E}[{\epsilon }^2]=\mathrm{Var}[e]+{(h-\mathrm{E}[f])}^2+\mathrm{E}\left[{(f-\mathrm{E}[f])}^2\right]}$
$$\mathrm{平}\mathrm{方}\mathrm{损}\mathrm{失}\mathrm{期}\mathrm{望}=\mathrm{噪}\mathrm{声}\mathrm{方}\mathrm{差}+\mathrm{偏}{\mathrm{误}}^2+\mathrm{模}\mathrm{型}\mathrm{方}\mathrm{差}$$

4、我们还可以写成：
${\displaystyle \mathcal{H}=\{f\mid p(y=f(\mathit{x})\mid \mathit{x},\mathcal{D})\}=\{f(\mathit{\beta })\mid p(y=f(\mathit{x};\mathit{\beta })\mid \mathit{x},\mathcal{D};\mathit{\beta }),\mathit{\beta }\in {\mathbb{R}}^k\}}$。这里的${\displaystyle \mathcal{H}}$是模型 $f$的集合。

2、这里的符号有一个重要的解释：

${\displaystyle y}$是一个随机变量，它的取值是 ${\displaystyle y=y_i}$。 ${\displaystyle \mathit{x}}$表示的是 ${\displaystyle n}$个 ${\displaystyle k}$维输入数据。也就是说 ${\displaystyle \mathit{x}}$也是一个变量，不过是向量的形式。它的取值是 ${\displaystyle \mathit{x}={\mathit{x}}_i}$。

3、换一个程序员比较好理解的说法：

${\displaystyle y,\mathit{x}}$是一个类。而 ${\displaystyle y_i,{\mathit{x}}_i}$是一个实例。所以一个实例 ${\displaystyle P(y_i\mid {\mathit{x}}_i,\mathcal{D})}$，又有 ${\displaystyle P(y_{n+1}\mid {\mathit{x}}_{n+1},\mathcal{D})}$是一个数或者一个概率。${\displaystyle \hat{y},{\hat{y}}_i}$也是类和实例的区别。

输出的最佳估计： ${\displaystyle \hat{y}=\hat{f}(x)=\underset{\hat{y}}{\text{argmax}}P(y=\hat{y}\mid \mathit{x},\mathcal{D})}$

4、算法空间

${\displaystyle \zeta \in \mathcal{L}}$，它是算法的集合。

5、参数空间

${\displaystyle \mathit{\beta }\in {\mathbb{R}}^k}$。这里的元素我们将 ${\displaystyle {\mathbb{R}}^k}$的k维有序组与向量矩阵$\underset{(k\times 1)}{\mathit{\beta }}$等同，以方便表达。

6、概念总结

有了这些基本概念，我们就可以建立起机器学习的基本框架。一张图搞定:

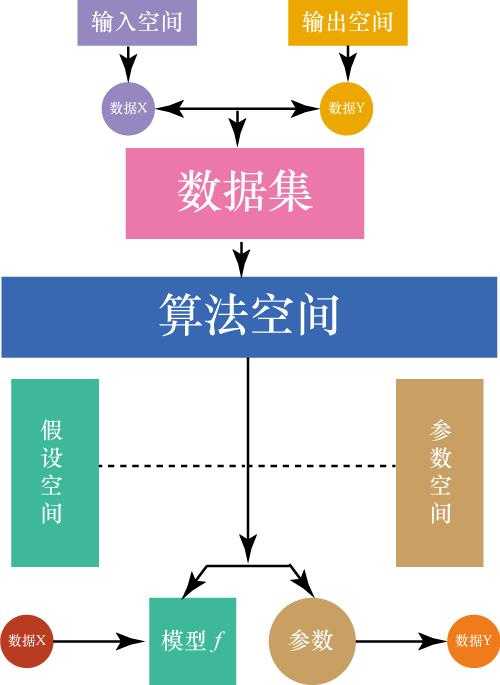
机器学习框架

7、指示函数，或者叫示性函数

${\displaystyle {\mathrm{I}}_x(A)=\{\begin{array}{ll}1& \text{if }x\in A\\ 0& \text{if }x\notin A\end{array}}$

8、评论

这段概论，大部分是站在频率学派的角度解释的，以后我们还会用贝叶斯学派的观点。

我们注意到符号与文字的转换要非常熟练，这就像英语，如果做到同声翻译的水平，这将有利于快速理解。所以一套好的数学符号是非常关键，好数学符号令人赏心悦目。但是每个人都有不同的风格，这就有点无语，以至于不同的书，符号不一样。TMD这是英语有了方言啊。有些书上的符号真是丑的不堪入目啊。严重影响阅读学习体验。

---

二、回归模型

1、线性回归模型：

模型的一些表示方法
$y_i={\mathit{x}}_i^T\mathit{\beta }+{ϵ}_i={\mathit{x}}_{i,:}^T\mathit{\beta }+{ϵ}_i$
$\mathit{y}=\mathit{X}\mathit{\beta }+\mathit{ϵ}$
$S={\mathit{ϵ}}^{\text{T}}\mathit{ϵ}$
模型矩阵解释：
$${\displaystyle \underset{(n\times 1)}{\mathit{y}}=\underset{n\times k}{\underbrace{\underset{(n\times k)}{\mathit{X}}\underset{(k\times 1)}{\mathit{\beta }}}}+\underset{(n\times 1)}{\mathit{ϵ}}}$$

2、梯度下降算法：$\mathit{\beta }:=\mathit{\beta }-\alpha \mathrm{\nabla }S$

梯度下降算法的本质：可以使用相图的思想加以理解。例如有关系${\displaystyle F(x,y,t)=0}$。如果我们画出
$$\{\begin{array}{l}\dot{x}=-3x+5y\\ \dot{y}=-5x-7\sin (y)\end{array}$$动力系统的相图。那么如果是凸函数。相图上的曲线集就会流向平衡点。如图

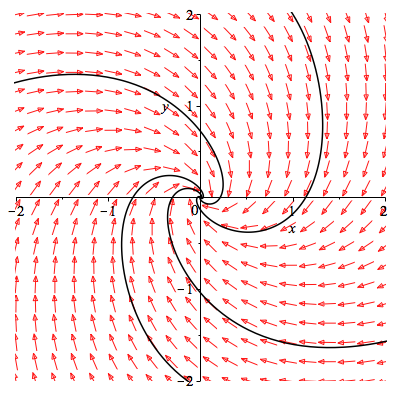
相图

所谓梯度就是图中的箭头乘以梯度的大小。代表了该点速度最快的方向。而 ${\displaystyle {\alpha }_k}$就是给梯度加了一个控制器。
所以应该能够理解梯度下降算法了：$${\mathit{\beta }}_{k+1}={\mathit{\beta }}_k-{\alpha }_k\mathrm{\nabla }S({\mathit{\beta }}_k)$$所以当系统比较复杂的时候，必然就面临问题。例如这种：
$$\{\begin{array}{l}\dot{x}=-x+y\\ \dot{y}=xy-1\end{array}$$这个系统就非常复杂了。初始位置不同，我们将走向完全不同的结局。

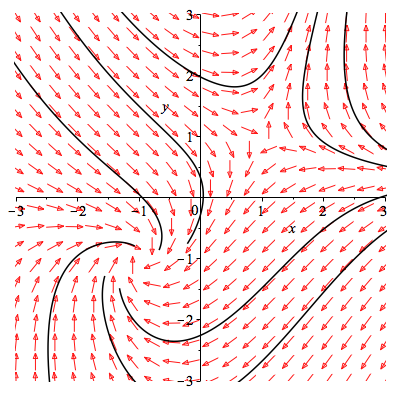
相图2

3、规范方程

规范方程的本质可以如下理解：

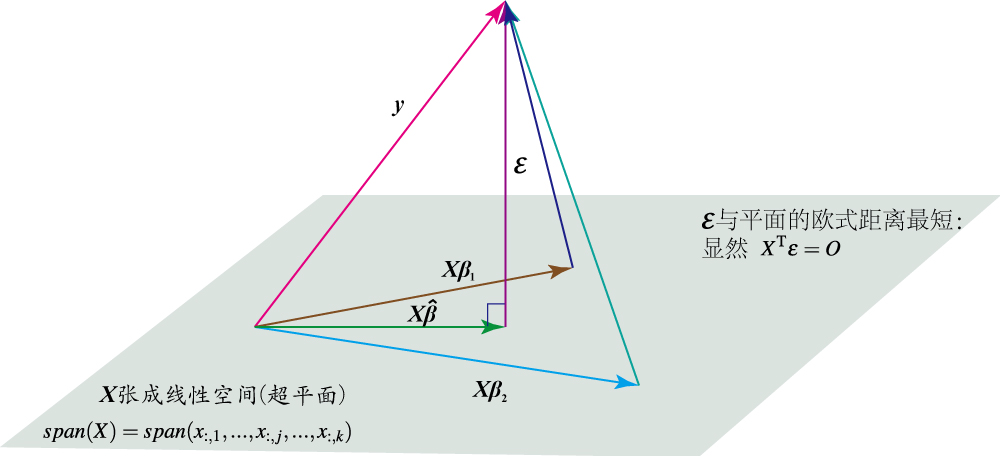
线性回归几何解释

解决学习平方误差 ${\displaystyle S}$的最小化问题：
$$\underset{\mathit{\beta }}{min}S={\mathit{ϵ}}^{\text{T}}\mathit{ϵ}$$简单推理易得：$\hat{\mathit{\beta }}=({\mathit{X}}^T\mathit{X}{)}^{-1}{\mathit{X}}^T\mathit{y}$

现在我们用线性空间的概念来加以理解：
${\displaystyle \mathit{X}}$张成的空间,或者说超平面 ${\displaystyle span(\mathit{X})=span({\mathit{x}}_{:,1},\dots ,{\mathit{x}}_{:,j},\dots ,{\mathit{x}}_{:,k})}$ 这里的 ${\displaystyle {\mathit{x}}_{:,j}=\left[\begin{array}{c}{x}_{1,j}\\ x_{2,j}\\ ⋮\\ x_{n,j}\end{array}\right]}$。如图我们很容发现要使得 ${\displaystyle \mathit{ϵ}}$的欧式距离最短。那么${\displaystyle \mathit{ϵ}}$必然与 ${\displaystyle span({\mathit{x}}_{:,1},\dots ,{\mathit{x}}_{:,jj},\dots ,{\mathit{x}}_{:,k})}$垂直。即有如下方程。
$${\mathit{X}}^T\mathit{ϵ}={\mathit{X}}^T(\mathit{y}-\mathit{X}\hat{\mathit{\beta }})=\mathbf{0}$$简单推理易得：$\hat{\mathit{\beta }}=({\mathit{X}}^T\mathit{X}{)}^{-1}{\mathit{X}}^T\mathit{y}$。所以 ${\displaystyle \mathit{y}}$的最佳估计量 ${\displaystyle \hat{\mathit{y}}}$是 ${\displaystyle \mathit{y}}$在${\displaystyle span({\mathit{x}}_{:,1},\dots ,{\mathit{x}}_{:,jj},\dots ,{\mathit{x}}_{:,k})}$空间上的投影。

---

注释：

[^1]: 如果 ${\displaystyle \zeta }$表示算法,可写为${\displaystyle P(y\mid \mathit{x},\mathcal{D},\zeta )}$

---

版权声明
	由引线小白创作并维护的柠檬CC博客采用署名-非商业-禁止演绎4.0国际许可证。 本文首发于柠檬CC [ https://www.limoncc.com ] , 版权所有、侵权必究。
本文永久链接	httpss://www.limoncc.com/post/72a5edcac04cd1a3e93a37ee90ac9259/

如果您需要引用本文，请参考：

引线小白. (Jan. 8, 2017). 《机器学习概论》[Blog post]. Retrieved from https://www.limoncc.com/post/72a5edcac04cd1a3e93a37ee90ac9259

@online{limoncc-72a5edcac04cd1a3e93a37ee90ac9259, title={机器学习概论}, author={引线小白}, year={2017}, month={Jan}, date={8}, url={\url{https://www.limoncc.com/post/72a5edcac04cd1a3e93a37ee90ac9259}}, }