作者: 引线小白-本文永久链接:httpss://www.limoncc.com/post/7a57a5a743894a0e/
知识共享许可协议: 本博客采用署名-非商业-禁止演绎4.0国际许可证
一、引言
RWKV模型是一种RNN范式下的大语言模型实现范式。效果是相当不错,关键它的训练和推理要求资源低。非常值得研究。这里给个翻译: 敏感加权键值模型(Receptance Weighted Key Value model)。由于作者还未发表[论文]^1(论文已出(2022-5-22)赶紧研究中)。这里只能借助源码来做一些分析。这篇文章就是笔者对源码分析和阅读论文的一些记录。希望对大家有所帮助。如有错误请大家指正。
二、从线性注意力到RNN
2.1、从AFT到RWKV
在AFT[^2]中对 $t$权重和对 $t-1$之前的权重是原则是一样的。而在RWKV中,对$t-1$之前权重是随序列衰减的。对 $t$权重是单独赋值了一个 $u$。
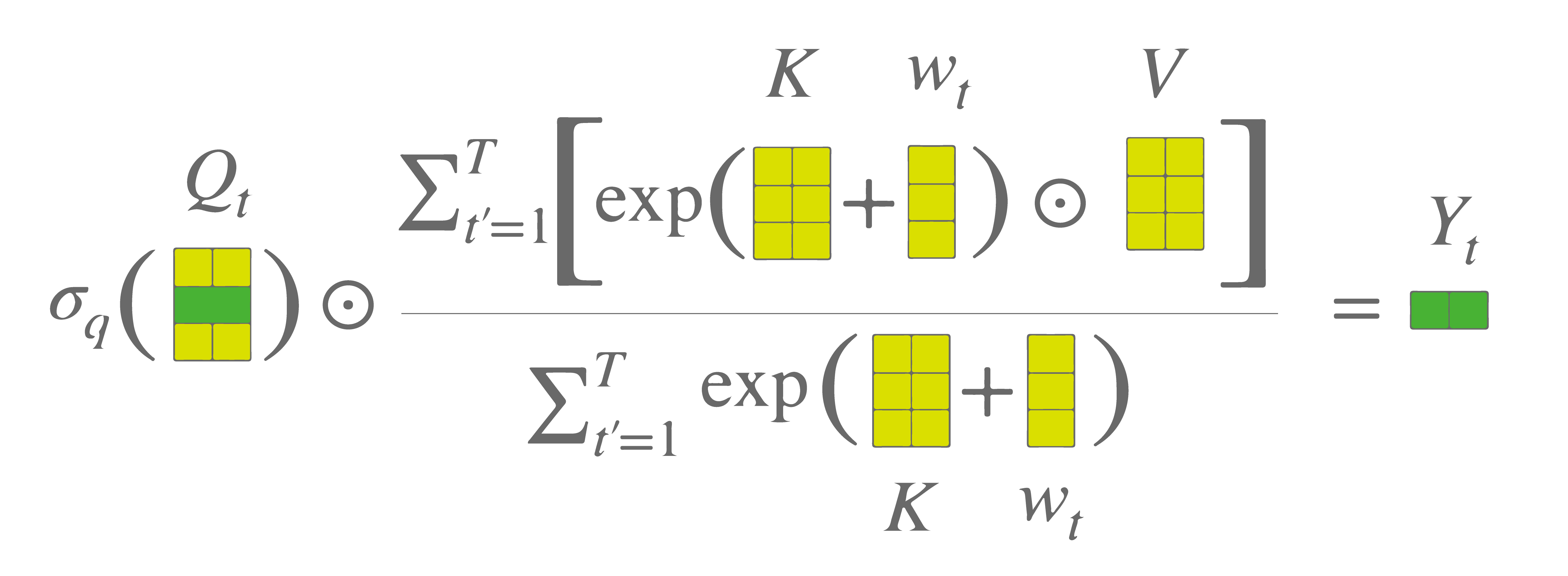
AFT
也就是说
$$\begin{align}
\bm{o}_t=\sigma(\bm{r}_t) \odot\bm{I}^\text{T}\big[\mathrm{softmax}\big(-w\cdot\mathrm{\bm{arange}}[0:t-1]+\bm{K}\big)\odot \bm{V}\big]
\end{align}$$
2.2、变换到RNN
$$\begin{align}
o_{t}=\sigma(r_t) \cdot\frac{\sum_{\tau=1}^{t-1} \exp\big[-{w(t-1-\tau)+k_\tau}\big]\cdot v_\tau+\exp\big[u+k_t\big]\cdot v_t}{\sum_{\tau=1}^{t-1} \exp\big[-{w(t-1-\tau)+k_\tau}\big]+\exp\big[u+k_t\big]}
\end{align}$$
为了便于分析,我们单独考察分子
$$\begin{align}
a_t^{out} &=\sum_{\tau=1}^{t-1} \exp\big[-{w(t-1-\tau)+k_\tau}\big]\cdot v_\tau+\exp\big[u+k_t\big]\cdot v_t\\
&=\exp[-w]\sum_{\tau=1}^{t-2} \exp\big[-{w(t-2-\tau)+k_\tau}\big]\cdot v_\tau+\exp[k_{t-1}]v_{t-1}+\exp\big[u+k_t\big]\cdot v_t
\end{align}$$
令 $\displaystyle a_{t-2}=\sum_{\tau=1}^{t-2} \exp\big[-{w(t-2-\tau)+k_\tau}\big]\cdot v_\tau$ 则有
$$\begin{align}
a_t^{out} &= \exp[-w]a_{t-2}+\exp[k_{t-1}]v_{t-1}+\exp\big[u+k_t\big]\cdot v_t\\
&=a_{t-1}+\exp\big[u+k_t\big]\cdot v_t
\end{align}$$
这样我们改为递推RNN的形式就是
1、Initialize $\displaystyle a_0=0,b_0=0$
2、Output
$\displaystyle
\qquad\qquad\begin{array}{|lc}
a_t^{out} =a_{t-1}+\exp[u+k_t]\cdot v_t \\
b_t^{out} =b_{t-1}+\exp[u+k_t]\\
wkv_t= a_t^{out}/b_t^{out}\\
o_t=\sigma(r_t)\cdot wkv_t
\end{array}\\$
3、Update the state
$\displaystyle
\qquad\qquad\begin{array}{|lc}
a_t =\exp[-w]a_{t-1}+\exp[k_t]\cdot v_t \\
b_t =\exp[-w]b_{t-1}+\exp[k_t]\\
\end{array}\\$
3、# end
三、时间混合机制
3.1、基本框架
3.2、上溢与代码实现
RWKV模型V4的代码实现和原理公式是不一样的。融入了一个溢出的技巧,这导致原理公式的脱节代码实现。因为这不太容易看出是等价的。下面文本提供一个证明。这个证明笔者最早发布在(如何评价最新的RWKV论文 (arXiv 2305.13048)?)的知乎问答中。
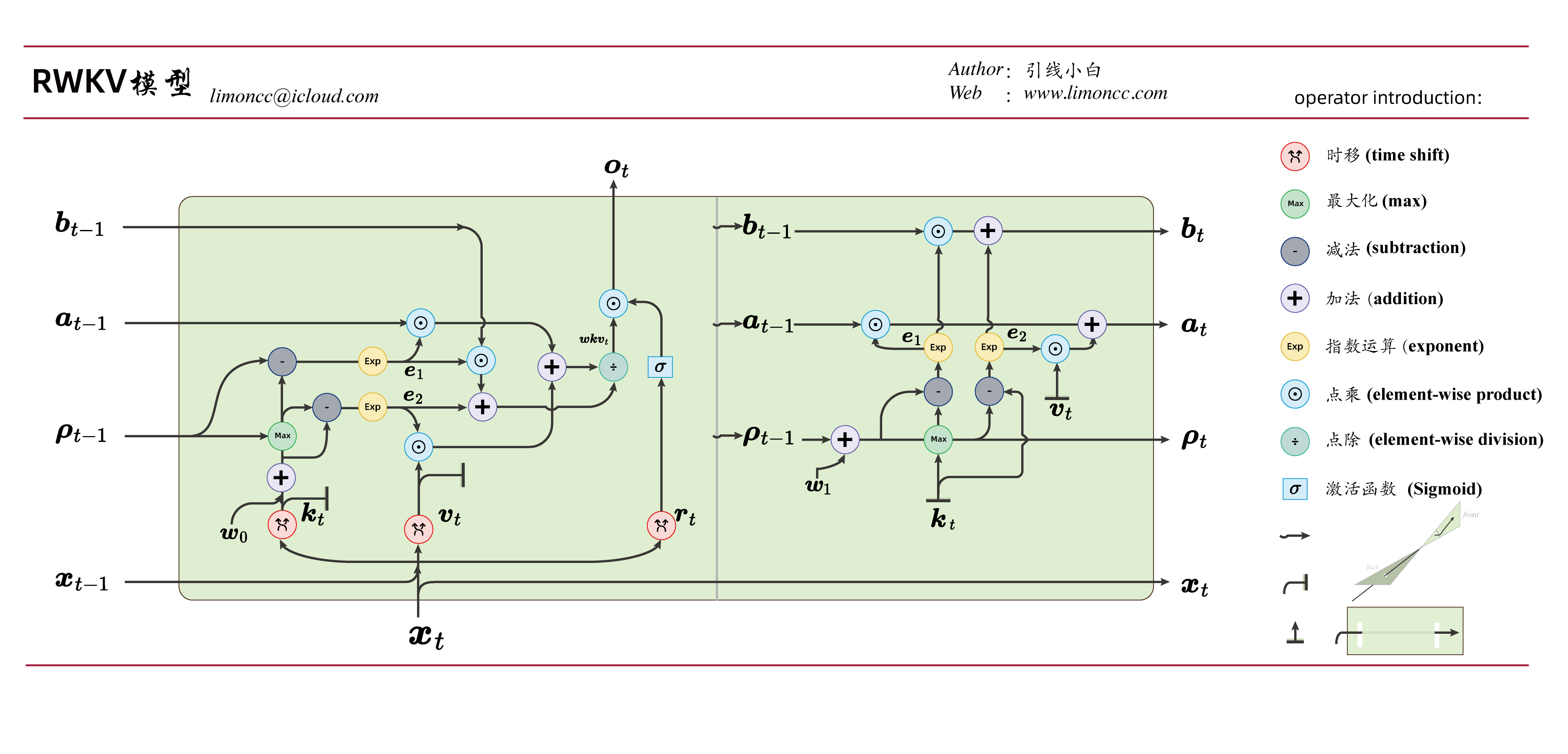
RWKV模型V4
RWKV模型V4的代码实现和原理公式的等价性证明:下面我们来分析一下如何避免 $\displaystyle \exp[k_t]$向上溢出的技巧。为了简化分析我们近看一个词元(token)的一个维度(通道)计算。要防止 $\displaystyle\displaystyle \exp[k_t]$上溢出,显然这个时候 $\displaystyle k_t$是一大数。这个时候,我们给他减去一个一样大的数 $\displaystyle q$就可以了。注意 $\displaystyle q=k_t+\delta$。 只要确保 $\displaystyle \displaystyle \exp[\delta] $不会溢出即可,这样有:
$$\begin{align}
o_{t}=\sigma(r_t) \cdot\frac{\sum_{\tau=1}^{t-1} \exp\big[-{w(t-1-\tau)+k_\tau-q}\big]\cdot v_\tau+ \exp\big[u+k_t-q\big]\cdot v_t}{\sum_{\tau=1}^{t-1} \exp\big[-{w(t-1-\tau)+k_\tau-q}\big]+ \exp\big[u+k_t-q\big]}
\end{align}$$
为了便于分析,我们单独考察分子
$$\begin{align}
a_t^{out}&=\sum_{\tau=1}^{t-1} \exp\big[-{w(t-1-\tau)+k_\tau-q}\big]\cdot v_\tau+\exp\big[u+k_t-q\big]\cdot v_t\\
&=\exp[-w]\sum_{\tau=1}^{t-2} \exp\big[-{w(t-2-\tau)+k_\tau-q}\big]\cdot v_\tau+\exp\big[k_{t-1}-q\big]\cdot v_{t-1}+\exp\big[u+k_t-q\big]\cdot v_t\\
&=\exp[-q]\bigg[\exp[-w]\cdot a_{t-2}+\exp\big[k_{t-1}\big]\cdot v_{t-1}\bigg]+ \exp\big[u+k_t-q\big]\cdot v_t
\end{align}$$
为了规避 $\displaystyle \exp[k_{t-1}] $溢出,我们也需要一个 $\displaystyle \exp[-\rho_{t-1}]$ 这样有
$$\begin{align}
a_t^{out}&=\exp\big[\rho_{t-1}-q\big]\big[\exp[-w-\rho_{t-1}]\cdot a_{t-2}+\exp\big[k_{t-1}-\rho_{t-1}\big]\cdot v_{t-1}\big]+\exp\big[u+k_t-q\big]\cdot v_t
\end{align}$$
同时 $\displaystyle \exp[-w-\rho_{t-1}]$也有溢出风险,于是我们可以添加一个 $\displaystyle \exp[\rho_{t-2}] $这样有
$$\begin{align}
a_t^{out}&=\exp\big[\rho_{t-1}-q\big]\big[\exp[\rho_{t-2}-w-\rho_{t-1}]\cdot \exp[-\rho_{t-2}] a_{t-2}+\exp\big[k_{t-1}-\rho_{t-1}\big]\cdot v_{t-1}\big]+\exp\big[u+k_t-q\big]\cdot v_t
\end{align}$$
我们令 $\displaystyle \tilde{a}_{t-2}=\exp[-\rho_{t-2}] a_{t-2}$,这样发现
$$\begin{align}
\tilde{a}_{t-1}&=\exp[-\rho_{t-1}] a_{t-1}\\
&=\exp[-\rho_{t-1}] \big(\exp[-w]a_{t-2}+\exp[k_{t-1}]\cdot v_{t-1}\big)\\
&=\exp[-w-\rho_{t-1}]a_{t-2}+\exp[k_{t-1}-\rho_{t-1}]\cdot v_{t-1}\\
&=\exp[-\rho_{t-1}] \big(\exp[-w]\exp[\rho_{t-2}]\tilde{a}_{t-2}+\exp[k_{t-1}]\cdot v_{t-1}\big)\\
&=\exp[\rho_{t-2}-w-\rho_{t-1}]\tilde{a}_{t-2}+\exp[k_{t-1}-\rho_{t-1}]\cdot v_{t-1}
\end{align}$$
这样就有
$$\begin{align}
a_t^{out}=\exp\big[\rho_{t-1}-q\big]\tilde{a}_{t-1}+\exp\big[u+k_t-q\big]\cdot v_t
\end{align}$$
$$\begin{align}
\tilde{a}_{t}=\exp[\rho_{t-1}-w-\rho_{t}]\tilde{a}_{t-1}+\exp[k_{t}-\rho_{t}]\cdot v_{t}
\end{align}$$
下面我们开始最后征程,给 $\displaystyle q$和 $\displaystyle \rho_t$给一个恰当具体的值。事实上我们有, 对于 $\displaystyle \tilde{a}_t=\exp[-\rho_t] a_t$
$$\begin{align}
a_1&=\exp[k_1]v_1\\
b_1&=\exp[k_1]
\end{align}$$
我们可以令 $\displaystyle \rho_1=k_1$
这样我们就有新的递推公式,未来规避溢出bug,我们先后做了三次修正,此外还有 $\displaystyle \exp[\rho_{t-1}-q]$
$$\begin{align}
\unicode{x2776}&\;\exp[-q]\longrightarrow \exp[u+k_t-q]\\
\unicode{x2777}&\;\exp[\rho_{t-1}]\longrightarrow \exp[k_{t-1}-\rho_{t-1}]\\
\unicode{x2778}&\;\exp[\rho_{t-2}]\longrightarrow \exp[\rho_{t-2}-w-\rho_{t-1}]\\
\unicode{x2776}\unicode{x2777}&\;\exp[\rho_{t-1}-q]
\end{align}$$
解决问题的答案就蕴含在解决问题的过程中的。特别的,对于 $\displaystyle x\leqslant =0 $有 $\displaystyle f(x)=\exp[x] \in (0,1]$。考虑到sub-max算子
$$\begin{align}
\mathrm{submax}(x,y): = x-max(x,y)\leqslant 0
\end{align}$$
对于 $\displaystyle \exp[\rho_{t-2}-w-\rho_{t-1}]=\exp\big[\mathrm{submax}(\rho_{t-2}-w,A)\big]$,也就是说 $\displaystyle \rho_{t-1} = \max(\rho_{t-2}-w,A)$。同理我们就有如下这些
$$\begin{align}
\exp[\rho_{t-2}-w-\rho_{t-1}]=\exp\big[\mathrm{submax}(\rho_{t-2}-w,A)\big]&\to \rho_{t-1} = \max(\rho_{t-2}-w,A)\\
\exp[\rho_{t-1}-q]=\exp\big[\mathrm{submax}(\rho_{t-1},B)\big]&\to q=\max(\rho_{t-1},B)\\
\exp[k_{t-1}-\rho_{t-1}]=\exp\big[\mathrm{submax}(k_{t-1}-C)\big]&\to
\rho_{t-1}=\max(k_{t-1},C)\\
\exp[u+k_t-q]=\exp\big[\mathrm{submax}(u+k_t,D)\big]&\to
q=\max(u+k_t,D)
\end{align}$$
易得
$$\begin{align}
q=\max(\rho_{t-1},u+k_t)\\
\rho_{t-1}=\max(\rho_{t-2}-w,k_{t-1})
\end{align}$$
这样我们就有新的递推RNN,也就证明了理论公式与防溢公式的等价性。
1、Initialize
$\displaystyle
\qquad\qquad\begin{array}{|lc}
\rho_1=k_1\\
\tilde{a}_1=\exp[-\rho_1] a_1=v_1\\
\tilde{b}_1=\exp[-\rho_1] b_1=1
\end{array}\\$
2、Output
$\displaystyle
\qquad\qquad\begin{array}{|lc}
q=\max(\rho_{t-1},u+k_t)\\
a_t^{out} =\exp\big[\rho_{t-1}-q\big]\tilde{a}_{t-1}+\exp\big[u+k_t-q\big]\cdot v_t \\
b_t^{out} =\exp\big[\rho_{t-1}-q\big]\tilde{b}_{t-1}+\exp\big[u+k_t-q\big]\\
wkv_t= a_t^{out}/b_t^{out}\\
o_t=\sigma(r_t)\cdot wkv_t
\end{array}\\$
3、Update the state
$\displaystyle
\qquad\qquad\begin{array}{|lc}
\rho_{t}=\max(\rho_{t-1}-w,k_t)\\
\tilde{a}_t =\exp[\rho_{t-1}-w-\rho_{t}]\tilde{a}_{t-1}+\exp[k_{t}-\rho_{t}]\cdot v_{t} \\
\tilde{b}_t =\exp[\rho_{t-1}-w-\rho_{t}]\tilde{b}_{t-1}+\exp[k_{t}-\rho_{t}]\\
\end{array}\\$
3、# end
具体代码实现可以参考RWKV_in_150_lines。
四、通道混合机制
RWKV使用通道混合机制代替了transforms的FFN,特别的是使用的平方和门控制机制。起着放大和筛选机制。
$$\begin{align}
o_t = \sigma(r_t)\odot \big[W_v\cdot \mathrm{ReLU}^2(k_t,0)\big]
\end{align}$$
五、基本架构
模型架构基本和transforms一致。整体是就是时间混合、通道混合、残差连接、层归一化的不断堆叠。
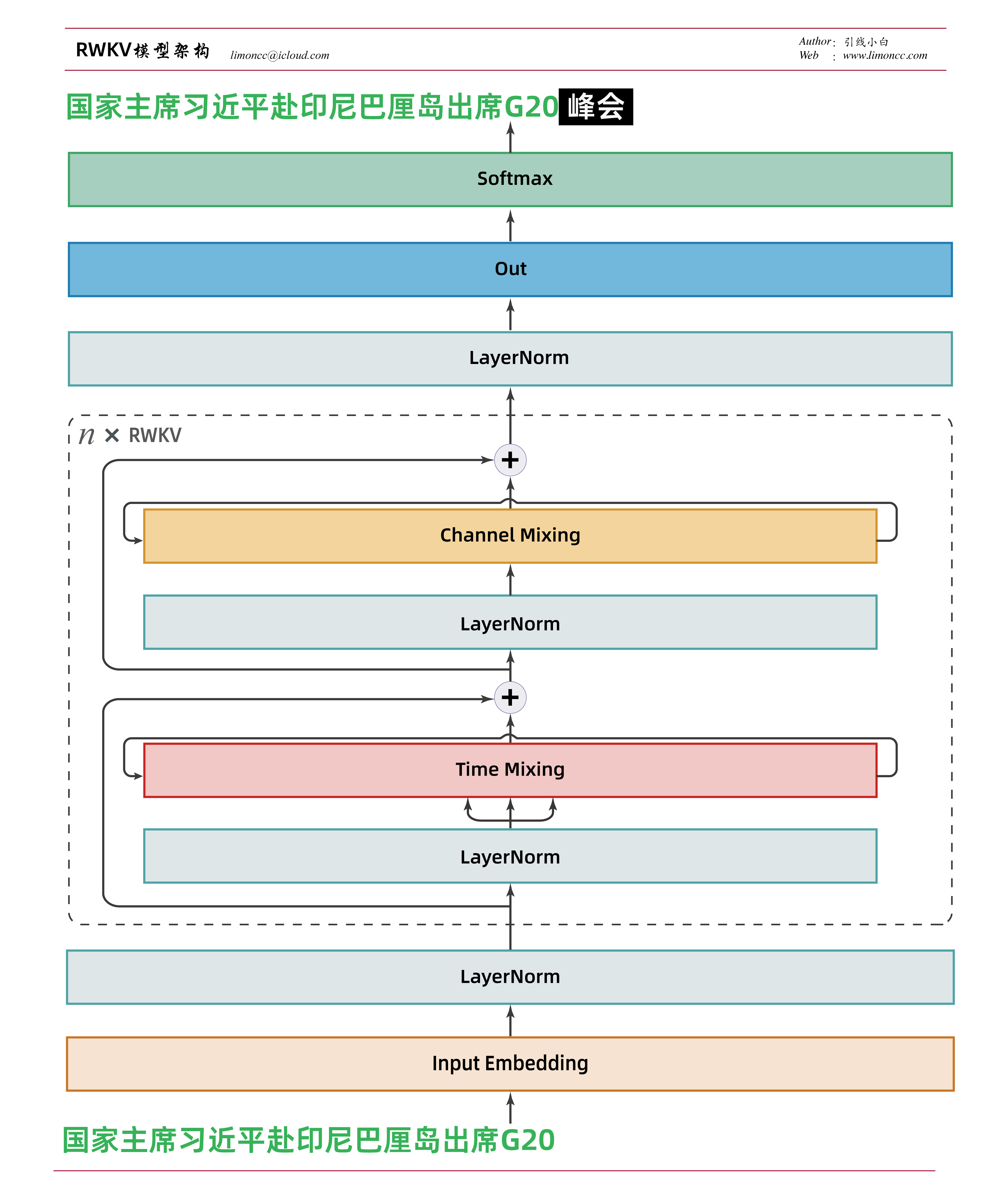
RWKV模型架构
[^1]: Peng, B., Alcaide, E., Anthony, Q., Albalak, A., Arcadinho, S., Cao, H., et al. (n.d.). RWKV: Reinventing RNNs for the Transformer Era.
[^2]: Zhai, S., Talbott, W., Srivastava, N., Huang, C., Goh, H., Zhang, R., & Susskind, J. (2021, September 21). An Attention Free Transformer. arXiv. http://arxiv.org/abs/2105.14103. Accessed 30 May 2023
| 版权声明 |  |
| 由引线小白创作并维护的柠檬CC博客采用署名-非商业-禁止演绎4.0国际许可证。 本文首发于柠檬CC [ https://www.limoncc.com ] , 版权所有、侵权必究。 | |
| 本文永久链接 | httpss://www.limoncc.com/post/7a57a5a743894a0e/ |
| 如果您需要引用本文,请参考: |
| 引线小白. (May. 18, 2023). 《理解RWKV模型一_大语言模型研究01》[Blog post]. Retrieved from https://www.limoncc.com/post/7a57a5a743894a0e |
| @online{limoncc-7a57a5a743894a0e, title={理解RWKV模型一_大语言模型研究01}, author={引线小白}, year={2023}, month={May}, date={18}, url={\url{https://www.limoncc.com/post/7a57a5a743894a0e}}, } |