作者: 引线小白-本文永久链接:httpss://www.limoncc.com/post/875b887a5e7e39e56eea929a72336d4e/
知识共享许可协议: 本博客采用署名-非商业-禁止演绎4.0国际许可证
摘要:本文意在理清机器学习的基础问题。若有错误,请大家指正。
关键词:无向图,哈默斯利-克利福德定理,条件随机场
[TOC]
一、哈默斯利-克利福德定理Hammersley-Clifford定理
由于没有与无向图相关的拓扑排序,我们不能使用链式法则来表示 $ p \big(\bm{x}\big)$。因此,我们将概率密度与每个节点关联起来替换方法是,将势函数或因子与图中每个极大团联系起来。我们将团 $ c$势函数记为 $ \psi_c \big(\bm{x}_c\mid \bm{\theta}_c\big)$。势函数可以是其参数的任何非负函数。然后定义联合分布与团势函数乘积成比例。令人惊讶的是,可以通过这样的方式来表示任何可以由无向图模型表达条件独立性质的正分布。我们更正式地陈述这个结果如下
【 Hammersley-Clifford 定理】
一个正分布 $ p \big(\bm{x}\big)>0$ 能满足一个无向图模型 $ \mathcal{G}$的条件独立性质,当且仅当 $ p$能够被每个极大团因子的乘积表示。
$$\begin{align}
\forall x\to p(x)>0\Rightarrow \mathcal{I}(p)=\mathcal{I}(\mathcal{G})
\iff p \big(\bm{x}\mid \bm{\theta}\big)=\frac{1}{Z(\bm{\theta})}\prod_{c\in \mathcal{C}}\psi_c \big(\bm{x}_c\mid \bm{\theta}_c\big)
\end{align}$$
其中 $ \mathcal{C}$是图 $ \mathcal{G}$ 所有极大团的集合。 $ Z(\bm{\theta})$是配分函数:
$$\begin{align}
Z(\bm{\theta})=\sum_{\bm{x}}\prod_{c\in \mathcal{C}}\psi_c \big(\bm{x}_c\mid \bm{\theta}_c\big)
\end{align}$$
请注意,配分函数确保了整体分布总和为 $ 1$。
二、条件随机场Conditional random fields (CRFs)
2.1、一般定义
条件随机场conditional random field(CRF) (Lafferty et al . 2001年),又称判别随机场 (Kumar and Hebert 2003),是 MRF 的一个版本,其中所有团势以输入特征为条件:
$$\begin{align}
p \big(\bm{z}\mid \bm{X},\bm{w}\big)
=\frac{1}{Z \big(\bm{X},\bm{w}\big)}\prod_{c\in \mathcal{C}} \psi_c \big(\bm{z}_c\mid \bm{X},\bm{w}\big)
\end{align}$$
CRF 可以被认为是逻辑回归的结构化输出扩展,在此模型中,我们对输入特征的输出标签之间的关联进行建模。我们通常会假设一个对数线性表示的势能:
$$\begin{align}
\psi_c \big(\bm{z}_c\mid \bm{X},\bm{w}\big)
=\exp \big[\bm{w}_c ^\text{T} \bm{\phi} \big(\bm{X},\bm{z}_c\big)\big]
\end{align}$$
其中 $ \bm{\phi} \big(\bm{X},\bm{z}_c\big)$是一个由全局输入 $ \bm{X}$和局部标签 $ \bm{z}_c$所衍生的特征向量。
为了方便描述,我们形式化的定义隐变量数据集 $\displaystyle \mathcal{D}_T^z=\{z_t\}_{t=1}^T$,观测变量数据集$\displaystyle \mathcal{D}_T^{\bm{x}}=\{\bm{x}_t\}_1^T=:\bm{X}=[\bm{x}_1,\cdots,\bm{x}_T]^T$, 完全数据集$\displaystyle \mathcal{D}^+_T=\{\mathcal{D}_T^z,\mathcal{D}_T^\bm{x}\}$, 条件数据集 $\displaystyle \mathcal{D}^{\cdot|\cdot}_T=\{\mathcal{D}_T^\bm{x}\mid\mathcal{D}_T^z\}$ 。于是有
$$\begin{align}
p\big(\bm{z}\mid\bm{X}\big)
&=p\big(\mathcal{D}^{\cdot|\cdot}_T\big)
=p\big(\mathcal{D}_T^z\mid\mathcal{D}_T^\bm{x}\big)
=\frac{1}{Z \big(\bm{X}\big)}\prod_{c\in \mathcal{C}} \psi_c \big(\bm{z}_c\mid \bm{X},\bm{w}\big)\\
&=\frac{1}{Z \big(\bm{X}\big)}\prod_{c\in \mathcal{C}}\exp \big[\bm{w}_c ^\text{T} \bm{\phi} \big(\bm{X},\bm{z}_c\big)\big]\\
\end{align}$$
其中
$\displaystyle Z(\bm{X})=\sum_{\bm{z}\in \mathcal{Z}}\prod_{c\in \mathcal{C}}\exp \big[\bm{w}_c ^\text{T} \bm{\phi} \big(\bm{X},\bm{z}_c\big)\big]$
2.2、边势能和节点势能
为了让符号与原理更加清晰,我们来明确定义一下势能函数 $\displaystyle \exp \big[\bm{w}_c ^\text{T} \bm{\phi} \big(\bm{X},\bm{z}_c\big)\big]$:注意到条件随机场的极大团 $\displaystyle \{z_{t-1},z_t\}_{2}^T,\{z_t,\bm{X}\}_1^T$,我们分别定义边势能,和节点势能。或者叫转移分数,和发射分数。同时为简单记我们直接不同参数 $\displaystyle \lambda,\mu $融入到相应函数中, 进一步也可以把指数符号 $\displaystyle \exp$融入到相应函数中,于是有
$$\begin{align}
\exp \big[\bm{w}_c ^\text{T} \bm{\phi} \big(\bm{X},\bm{z}_c\big)\big]
&=\exp\big[[\lambda,\mu][s(z_{t-1},z_t,\bm{X}),k(z_t,\bm{X})]^T\big]\\
&=\exp\big[\lambda s(z_{t-1},z_t,\bm{X})+ \mu k(z_t,\bm{X}) \big]\\
& :\Rightarrow\exp\big[s(z_{t-1},z_t,\bm{X})+k(z_t,\bm{X}) \big]\\
& :\Rightarrow s\big(z_{t-1},z_t,\bm{X}\big)k\big(z_t,\bm{X}\big)
\end{align}$$
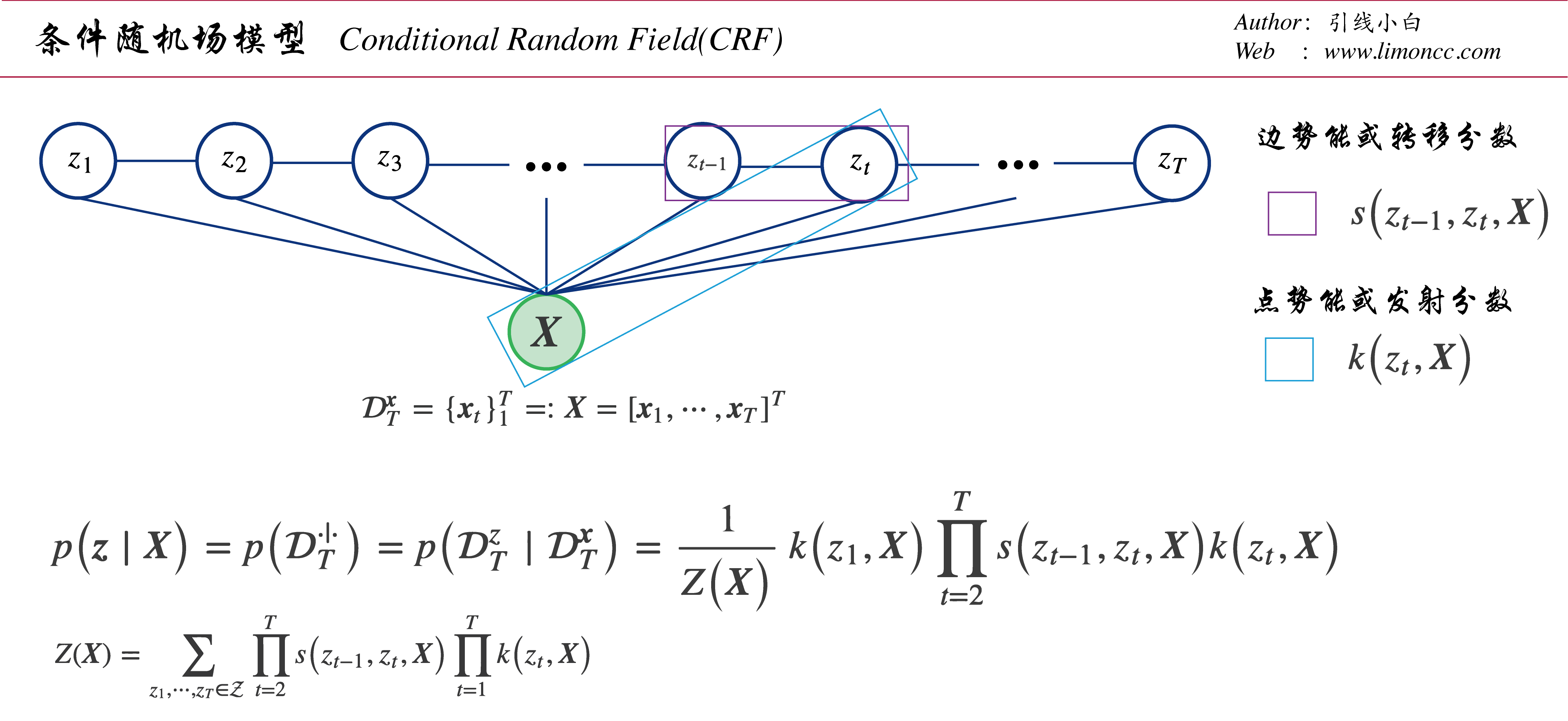
图: 条件随机场模型
代入,我们得到一个更加简洁,清晰的条件数据分布,
$$\begin{align}
p\big(\bm{z}\mid\bm{X}\big)
&=p\big(\mathcal{D}^{\cdot|\cdot}_T\big)
=p\big(\mathcal{D}_T^z\mid\mathcal{D}_T^\bm{x}\big)
=\frac{1}{Z\big(\bm{X}\big)}\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)\prod_{t=1}^Tk\big(z_t,\bm{X}\big)\\
&=\frac{1}{Z\big(\bm{X}\big)}k\big(z_1,\bm{X}\big)\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)k\big(z_t,\bm{X}\big)\\
\end{align}$$
其中
$\displaystyle Z(\bm{X})=\sum_{z_{1},\cdots,z_T\in \mathcal{Z}}\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)\prod_{t=1}^Tk\big(z_t,\bm{X}\big)$
为了简洁记,我们来定义一些符号。考虑隐变量有 $\displaystyle C$个状态 $\displaystyle z_t\in\{1,\cdots,C\}=\mathcal{Z}$,观测变量有 $\displaystyle O$个状态 $\displaystyle \bm{x}_t\in\{1,\cdots,O\}=\mathcal{X}$. 如果是文本,就是有多少个词。注意这里形式化的使用 $ o$来表示向量 $ \bm{x}_t$的状态,也就是说我们并没有定义向量是什么,因为这样能节约符号,和叙述上不必要的麻烦。继续定义若干参数:
$\displaystyle \pi[v]=k\big(z_1=v,\bm{X}\big)$
$\displaystyle A_t[i,j]=s\big(z_{t-1}=i,z_t=j,\bm{X})$
$\displaystyle \rho_t[j]=k\big(z_t=j,\bm{X})$
令参数集合为:
$$\begin{align}
\bm{\theta}=\{\bm{\pi},\bm{A}\}
\end{align}$$
注意在实际应用中,我们会加 $\displaystyle \log$,避免数据上溢,和下溢:$\displaystyle s\big(z_{t-1},z_t,\bm{X}\big) = \exp\big[\ln A_t[i,j]\big]$、$\displaystyle k\big(z_t,\bm{X}\big) = \exp\big[\ln \rho_t[j]\big]$。同时 $\displaystyle \pi[v]$中的 $v$一般指的是标签 $\displaystyle
三、前向向后算法
3.1、直接计算
我们要解决如何高效求条件数据集分布的问题,下面我们要分析一下这个基本问题。
$$\begin{align}
p\big(\mathcal{D}^{\cdot|\cdot}_T,\bm{\theta} \big)
&=p\big(\mathcal{D}_T^z\mid\mathcal{D}_T^\bm{x}, \bm{\theta} \big)
=\frac{1}{Z\big(\bm{X}\big)}k\big(z_1,\bm{X}\big)\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)k\big(z_t,\bm{X}\big)\\
&=\frac{1}{Z\big(\bm{X}\big)}\pi[v]\prod_{t=2}^TA_t[i,j]\rho_t[j]
\end{align}$$
我们取对数有
$$\begin{align}
\ln p\big(\mathcal{D}^{\cdot|\cdot}_T\mid \bm{\theta} \big)
&=\ln p\big(\mathcal{D}_T^z\mid\mathcal{D}_T^\bm{x},\bm{\theta} \big)
=\ln\bigg[\frac{1}{Z\big(\bm{X}\big)}\pi[v]\prod_{t=2}^TA_t[i,j]\rho_t[j]\bigg]\\
&=\underbrace{\mathop{\ln \pi[v]+\sum_{t=2}^T\big[\ln A_t[i,j]+\ln \rho_t[j]\big]}}_{\ln\text{true path}} - \underbrace{\mathop{\ln Z(\bm{X})}}_{\ln\text{total path}}
\end{align}$$
在给定条件数据集 $\displaystyle \mathcal{D}^{\cdot|\cdot}_T=\{\mathcal{D}_T^\bm{x}\mid\mathcal{D}_T^z\}=\{\bm{x}_1,\cdots,\bm{x}_T\mid z_1,\cdots,z_T\}$,条件数据集分布的计算分为两部分:
$$\begin{align}
\ln\text{true_path} = \ln \pi[v]+\sum_{t=2}^T\big[\ln A_t[i,j]+\ln \rho_t[j]\big]
\end{align}$$
计算复杂度是 $\displaystyle O(2T)$。为什么取名 true path和 total path,如下图:
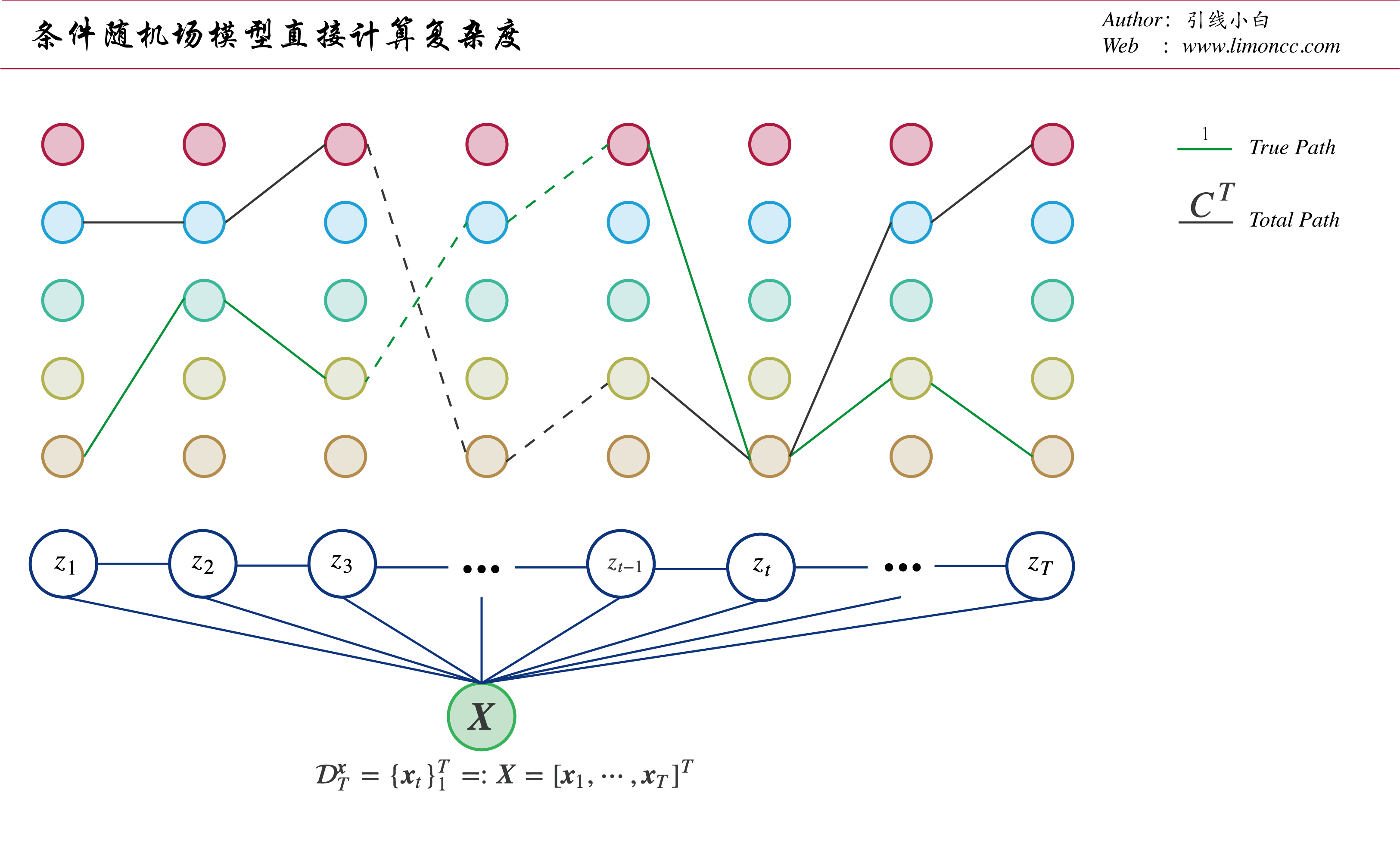
图: 条件随机场直接计算复杂度
难点在于第二部的计算
$$\begin{align}
\ln\text{total_path}
&= \ln Z(\bm{X})
= \ln \sum_{i,j\in \mathcal{Z}}\bigg[ \pi[v]\prod_{t=2}^TA_t[i,j]\rho_t[j]\bigg]\\
&=\ln \pi[v]+\ln\bigg[\underbrace{\mathop{\sum_{i,j\in \mathcal{Z}}\prod_{t=2}^T}}_{O(2TC^T)}A_t[i,j]\rho_t[j]\bigg]
\end{align}$$
这个方法的计算复杂度是 $\displaystyle O\big({2TC}^T\big)$, 例如 $\displaystyle C=5,T=10$,那么就要约计算 $\displaystyle 1.95\times10^8$已经非常夸张了。为了更快的计算条件分布,我们需要充分利用条件随机场的马尔可夫的性质。
3.2、前向计算
我们单独考虑 $\displaystyle \text{total_path}$: $\displaystyle Z(\bm{X})=\sum_{z_{1},\cdots,z_T\in \mathcal{Z}}\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)\prod_{t=1}^Tk\big(z_t,\bm{X}\big)$。
我们从序列的第 $\displaystyle 1$步看到第 $\displaystyle t$步,并令 $\displaystyle t$步状态为 $\displaystyle j$。这种操作也称为 sum-out。于是可以观测到
$$\begin{align}
\alpha_t[j]
&= \mathop{Z}^{\rightharpoonup}\big(\bm{X},z_t=j\big)\\
&=\sum_{z_1,\cdots,z_{t-1}\in \mathcal{Z}}k\big(z_1,\bm{X}\big)\prod_{\tau=2}^{t-1}\bigg[s\big(z_{\tau-1},z_\tau,\bm{X}\big)k\big(z_\tau,\bm{X}\big)\times s\big(z_{t-1},z_t=j,\bm{X}\big)k\big(z_t=j,\bm{X}\big)\bigg]\\
&=\sum_{z_{t-1}=i\in \mathcal{Z}}\sum_{z_1,\cdots,z_{t-2}\in \mathcal{Z}}k\big(z_1,\bm{X}\big)\prod_{\tau=2}^{t-2}\bigg[s\big(z_{\tau-1},z_\tau,\bm{X}\big)k\big(z_\tau,\bm{X}\big)
\times s\big(z_{t-2},z_{t-1}=i,\bm{X}\big)k\big(z_{t-1}=i,\bm{X}\big)\\&\times s\big(z_{t-1}=i,z_t=j,\bm{X}\big)k\big(z_t=j,\bm{X}\big)\bigg]\\
&=\sum_{z_{t-1}=i\in \mathcal{Z}}\Bigg[\sum_{z_1,\cdots,z_{t-2}\in \mathcal{Z}}\bigg[k\big(z_1,\bm{X}\big)\prod_{\tau=2}^{t-2}s\big(z_{\tau-1},z_\tau,\bm{X}\big)k\big(z_\tau,\bm{X}\big)\bigg]\\
&\times s\big(z_{t-2},z_{t-1}=i,\bm{X}\big)k\big(z_{t-1}=i,\bm{X}\big)\times s\big(z_{t-1}=i,z_t=j,\bm{X}\big)\Bigg]\\
&k\big(z_t=j,\bm{X}\big)\\
&=\sum_{z_{t-1}=i\in \mathcal{Z}}\alpha_{t-1}[i]A_t[i,j]\rho_t[j]
\end{align}$$
$$\begin{align}
\alpha_t[j]=\rho_t[j]\sum_{z_{t-1}=i\in \mathcal{Z}}\bigg[\alpha_{t-1}[i]\cdot A_t[i,j]\bigg]
\end{align}$$
易知道 $\displaystyle \alpha_1[i]=\pi[i]$,我们把它写成向量形式
$$\begin{align}
\bm{\alpha}_t = \bm{\rho}_t\odot\big[\bm{A}^T\bm{\alpha}_{t-1}\big]
\end{align}$$
这种操作也叫 sum-product的操作,即是我们把求和算子转化了乘积算子 $ \sum\to \prod$
于是 $\displaystyle \text{total_path}$就是
$$\begin{align}
\ln \text{total_path}
= \ln Z\big(\bm{X}\big)
= \ln \sum_{z_T=i\in \mathcal{Z}} \mathop{Z}^{\rightharpoonup}\big(\bm{X},z_T=i\big)
= \ln \sum_{i\in \mathcal{Z}}\alpha_{T}[i]
= \ln \bm{I}^T\bm{\alpha}_T
\end{align}$$
计算复杂变成了 $\displaystyle O\big(TS^2\big)$
3.3、前向后向算法
我们也可以反向从序列的第 $\displaystyle T$步看到第 $\displaystyle t$步,可以观测到
$$\begin{align}
\beta_t[i]
&=\mathop{Z}^{\leftharpoonup}\big(\bm{X},z_t=i\big)\\
&=\sum_{z_{t+1},\cdots,z_T\in \mathcal{Z}}s\big(z_{t}=i,z_{t+1},\bm{X}\big)k\big(z_{t+1},\bm{X}\big)\prod_{\tau=t+2}^{T}s\big(z_{\tau-1},z_\tau,\bm{X}\big)k\big(z_\tau,\bm{X}\big)\\
&=\sum_{z_{t+1}=j\in \mathcal{Z}}s\big(z_{t}=i,z_{t+1}=j,\bm{X}\big)k\big(z_{t+1}=j,\bm{X}\big)\\
&\sum_{z_{t+2},\cdots,z_T\in \mathcal{Z}}s\big(z_{t+1}=j,z_{t+2},\bm{X}\big)k\big(z_{t+2},\bm{X}\big)\prod_{\tau=t+3}^{T}s\big(z_{\tau-1},z_\tau,\bm{X}\big)k\big(z_\tau,\bm{X}\big)\\
&=\sum_{z_{t+1}=j\in \mathcal{Z}}s\big(z_{t}=i,z_{t+1}=j,\bm{X}\big)k\big(z_{t+1}=j,\bm{X}\big)\beta_{t+1}[j]\\
&=\sum_{z_{t+1}=j\in \mathcal{Z}}A_{t+1}[i,j]\rho_{t+1}[j]\beta_{t+1}[j]
\end{align}$$
即是
$$\begin{align}
\beta_t[i]=\sum_{z_{t+1}=j\in \mathcal{Z}}A_{t+1}[i,j]\rho_{t+1}[j]\beta_{t+1}[j]
\end{align}$$
写成矩阵形式有
$$\begin{align}
\bm{\beta}_t=\bm{A}\big[\bm{\rho}_{t+1}\odot \bm{\beta}_{t+1}\big]
\end{align}$$
于是 $\displaystyle \text{total_path}$就是
$$\begin{align}
\ln \text{total_path}
&= \ln Z\big(\bm{X}\big)
= \ln \sum_{z_t=i\in \mathcal{Z}} \mathop{Z}^{\rightharpoonup}\big(\bm{X},z_t=i\big)\mathop{Z}^{\leftharpoonup}\big(\bm{X},z_t=i\big)\\
&= \ln \sum_{i\in \mathcal{Z}}\alpha_{t}[i]\beta_t[i]
= \ln \bm{I}^T\big[\bm{\alpha}_t\odot\bm{\beta}_t\big]
\end{align}$$
这就是前向后向算法。
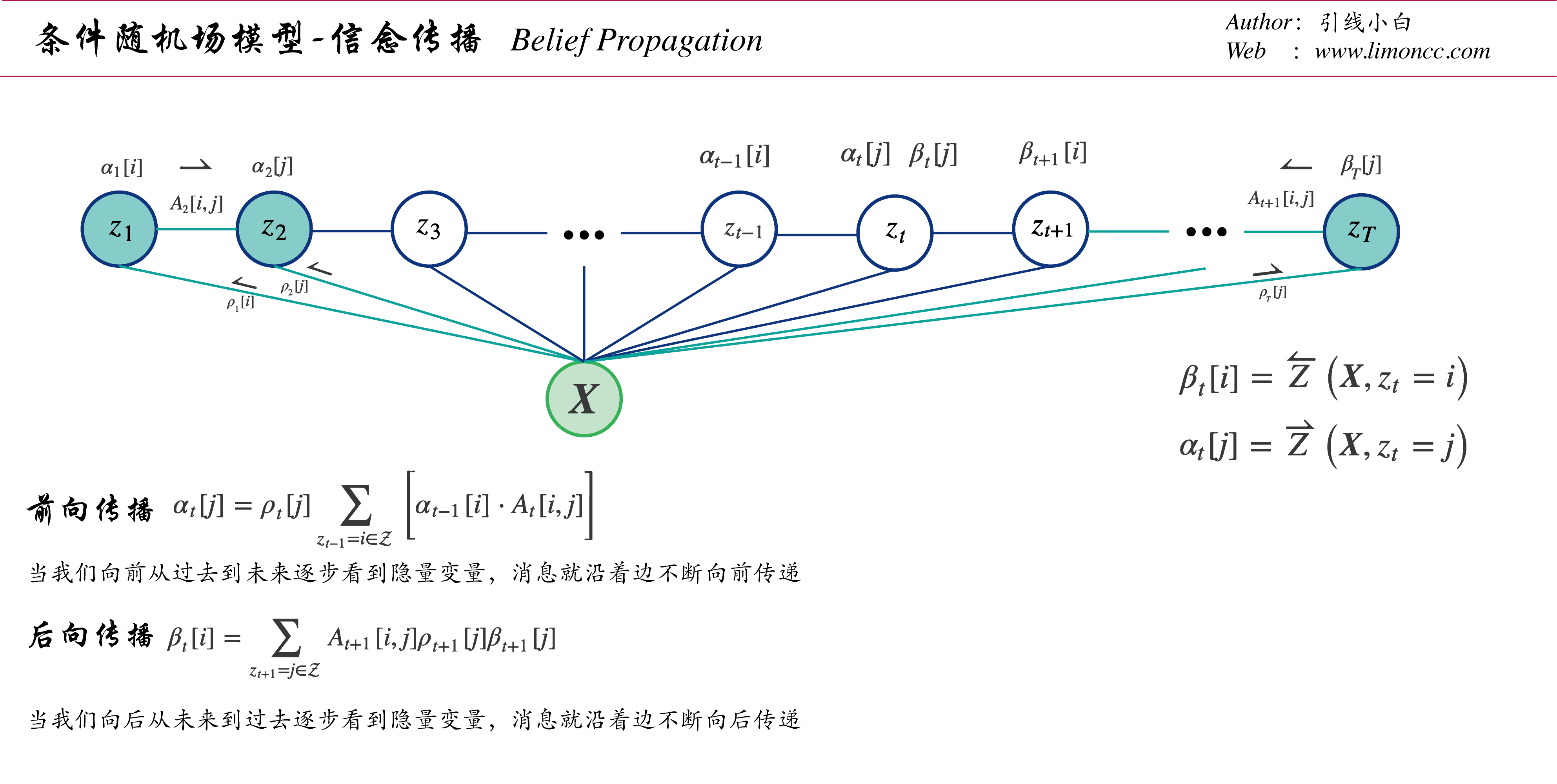
图: 条件随机场信念传播
3.4、一些概率与期望的计算
利用前向后向算法,很容实现一些计算:
1、条件概率
$$\begin{align}
p\big(z_t=i\mid\bm{X}\big)
&=p\big(z_t=i\mid \mathcal{D}_T^\bm{x}\big)
=\frac{\bm{\alpha}_t\odot\bm{\beta}_t}{\bm{I}^T\bm{\alpha}_t\cdot\bm{\beta}_t}\\
p\big(z_{t-1}=j,z_t=i\mid\bm{X}\big)
&=p\big(z_t=i\mid \mathcal{D}_T^\bm{x}\big)
=\frac{\bm{A}^T\bm{\alpha}_{t-1}\odot\bm{\beta}_t}{\bm{I}^T\bm{\alpha}_t\cdot\bm{\beta}_t}
\end{align}$$
2、期望值
$$\begin{align}
\mathrm{E}_{p\big(\mathcal{D}_T^z\mid\mathcal{D}_T^\bm{x}\big)}\bigg[s\big(z_{t-1},z_t,\bm{X}\big)\bigg]
&=\sum_{z_{t-1},z_t\in \mathcal{D}}s\big(z_{t-1},z_t,\bm{X}\big)
\frac{\alpha_{t-1}[z_{t-1}]A[z_{t-1},z_t]\beta_t[z_t]}{\bm{I}^T\bm{\alpha}_t\cdot\bm{\beta}_t}\\
\mathrm{E}_{p\big(\mathcal{D}_T^z\mid\mathcal{D}_T^\bm{x}\big)}\bigg[k\big(z_t,\bm{X}\big)\bigg]
&=\sum_{z_t\in \mathcal{D}}k\big(z_t,\bm{X}\big)
\frac{\alpha_{t}[z_{t}]\beta_t[z_t]}{\bm{I}^T\bm{\alpha}_t\cdot\bm{\beta}_t}
\end{align}$$
若有观测数据集经验分布 $\displaystyle \tilde{p}\big(\bm{X}\big)= \tilde{p}\big(\mathcal{D}_T^\bm{x}\big)$
$$\begin{align}
\mathrm{E}_{p\big(\mathcal{D}_T^z,\mathcal{D}_T^\bm{x}\big)}\bigg[s\big(z_{t-1},z_t,\bm{X}\big)\bigg]
&=\sum_{\bm{X}\in \mathcal{X}}\tilde{p}\big(\bm{X}\big)\sum_{z_{t-1},z_t\in \mathcal{D}}s\big(z_{t-1},z_t,\bm{X}\big)
\frac{\alpha_{t-1}[z_{t-1}]A[z_{t-1},z_t]\beta_t[z_t]}{\bm{I}^T\bm{\alpha}_t\cdot\bm{\beta}_t}\\
\mathrm{E}_{p\big(\mathcal{D}_T^z,\mathcal{D}_T^\bm{x}\big)}\bigg[k\big(z_t,\bm{X}\big)\bigg]
&=\sum_{\bm{X}\in \mathcal{X}}\tilde{p}\big(\bm{X}\big)\sum_{z_t\in \mathcal{D}}k\big(z_t,\bm{X}\big)
\frac{\alpha_{t}[z_{t}]\beta_t[z_t]}{\bm{I}^T\bm{\alpha}_t\cdot\bm{\beta}_t}
\end{align}$$
四、维特比算法
4.1、问题描述
维比特算法要解决的是求隐变量最可能状态序列。可以理解为:已知观测变量数据集,推断隐变量数据集。
$$\begin{align}
\widehat{\mathcal{D}}_T^z
=\widehat{\bm{z}}
=\mathop{\mathrm{argmax}}_{\mathcal{D}_T^z}p\big(\mathcal{D}_T^{\cdot\mid\cdot}\big)
=\mathop{\mathrm{argmax}}_{\mathcal{D}_T^z}p\big(\mathcal{D}_T^z\mid \mathcal{D}_T^\bm{x}\big)
=\mathop{\mathrm{argmax}}_{\bm{z}}p\big(\bm{z}\mid \bm{X}\big)
\end{align}$$
我们有条件数据集分布
$$\begin{align}
p\big(\mathcal{D}_T^z\mid\mathcal{D}_T^\bm{x} \big)
&=\frac{1}{Z\big(\bm{X}\big)}k\big(z_1,\bm{X}\big)\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)k\big(z_t,\bm{X}\big)\\
&=\frac{1}{Z\big(\bm{X}\big)}\pi[v]\prod_{t=2}^TA_t[i,j]\rho_t[j]
\end{align}$$
令 $\displaystyle g\big(\mathcal{D}_T^z,\mathcal{D}_T^\bm{x}\big)
=g\big(\bm{z},\bm{X}\big)
=k\big(z_1,\bm{X}\big)\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)k\big(z_t,\bm{X}\big)
=\pi[v]\prod_{t=2}^TA_t[i,j]\rho_t[j]$
则有,我们去掉了一个常数 $1/Z\big(\bm{X}\big)$,以简化计算。
$$\begin{align}
\widehat{\mathcal{D}}_T^z
&=\mathop{\mathrm{argmax}}_{\mathcal{D}_T^z}p\big(\mathcal{D}_T^z\mid \mathcal{D}_T^\bm{x}\big)
\propto \mathop{\mathrm{argmax}}_{\mathcal{D}_T^z}g\big(\mathcal{D}_T^z,\mathcal{D}_T^\bm{x}\big)
\end{align}$$
也就是说我们选择最大化
$$\begin{align}
\max_{\mathcal{D}_T^z}g\big(\mathcal{D}_T^z,\mathcal{D}_T^\bm{x}\big)
&=\max_{\mathcal{D}_T^z}\bigg[k\big(z_1,\bm{X}\big)\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)k\big(z_t,\bm{X}\big)\bigg]\\
&=\max_{\mathcal{D}_T^z}\bigg[\pi[i_1]\prod_{t=2}^TA_t[i_{t-1},i_{t}]\rho_t[i_{t}]\bigg]
\end{align}$$
其中 $\displaystyle i_t$是隐变量 $\displaystyle z_t$在时刻 $\displaystyle t$的状态。请反复体会这翻来覆去的表达式变换。不同的形式在不同场景下有利于说明不同的问题。
4.2、前向计算
我们可以拆分隐变量数据集 $\displaystyle \mathcal{D}_t^z=\mathcal{D}_{t-1}^z\cup\{z_t\}$,这一拆分的关键自觉是时刻 $\displaystyle 1 \rightsquigarrow t$的最可能路径必须是由 $\displaystyle 1 \rightsquigarrow t-1$的最可能路径组成的。问题就变成
$$\begin{align}
\max_{\mathcal{D}_t^z}g\big(\mathcal{D}_t^z,\mathcal{D}_t^\bm{x}\big)
&=\max_{z_t}\max_{\mathcal{D}_{t-1}^z}g\big(\mathcal{D}_{t-1}^z,z_t,\mathcal{D}_t^\bm{x}\big)
\end{align}$$
这种操作也称为 max-out.
已知条件数据集和模型参数,计算条件数据集分布概率的前向计算中我们使用了一种 sum-product的操作简化了问题,同样在维比特算法的前向计算中,我们也可以使用叫做 max-product的操作来简化问题。追寻这一思想,下面来具体分析一下。令时刻 $\displaystyle t$的状态为 $\displaystyle i_t$,进而定义路径 $\displaystyle \mathcal{D}_t^z=\mathcal{D}_{t-1}^z\cup\{z_t=i_t\}$的最大权重:
$$\begin{align}
\delta_t[i_t]=\max_{\mathcal{D}_{t-1}^z}g\big(\mathcal{D}_{t-1}^z,z_t,\mathcal{D}_t^\bm{x}\big)
\end{align}$$
我们继续拆分数据集:令时刻 $\displaystyle t-1$的状态为 $\displaystyle i_{t-1}$,于是有
$$\begin{align}
\delta_t[i_t]
&=\max_{\mathcal{D}_{t-1}^z}g\big(\mathcal{D}_{t-1}^z,z_t,\mathcal{D}_T^\bm{x}\big)\\
&=\max_{\mathcal{D}_{t-2}^z,z_{t-1}=i_{t-1}}\bigg[k\big(z_1,\bm{X}\big)\prod_{\tau=2}^{t-2}s\big(z_{\tau-1},z_\tau,\bm{X}\big)k\big(z_\tau,\bm{X}\big)
s\big(z_{t-2},z_{t-1}=i_{t-1},\bm{X}\big)k\big(z_{t-1}=i_{t-1},\bm{X}\big)\\
&\quad s\big(z_{t-1}=i_{t-1},z_{t}=i_{t},\bm{X}\big)k\big(z_{t}=i_{t},\bm{X}\big)
\bigg]\\
&=\max_{i_{t-1}}\delta_{t-1}[i_{t-1}]A[i_{t-1},i_t]\rho_t[i_t]
\end{align}$$
也就是说:时刻 $\displaystyle t$行至状态 $\displaystyle i_t$的最可能路径必须有是由时刻$\displaystyle t-1$行至其他状态 $\displaystyle i_{t-1}$的最可能路径中权重最大的那个。
$$\begin{align}
\delta_t[i_t]=\max_{i_{t-1}}\delta_{t-1}[i_{t-1}]A[i_{t-1},i_t]\rho_t[i_t]
\end{align}$$
写成矩阵形式固定 $\displaystyle i_t$,令$\displaystyle a[i_{t-1}]=A[i_{t-1},i_t]$则有
$$\begin{align}
\delta_t[i_t],\widehat{i}_{t-1}[z_t=i_t]
&=\max[\bm{\delta}_{t-1}\odot\bm{a}_{t-1}]\rho_t[i_t]\\
\bm{\delta}_t,\widehat{\bm{i}}_{t-1}
&=\big[\mathop{\mathrm{colmax}}[\bm{\delta}_{t-1}\odot\bm{A}]^\text{T}\odot\bm{\rho}_t
\end{align}$$
加上维度应该更容易理解
$$\begin{align}
\bm{\delta}_t,\widehat{\bm{i}}_{t-1}
&=\big[\underbrace{\mathop{\mathop{\mathrm{colmax}}[\underbrace{\mathop{\bm{\delta}_{t-1}}}_{1\times C}\odot\underbrace{\mathop{\bm{A}}}_{C \times C}}}_{C\times 1}\big]^\text{T}\odot\underbrace{\mathop{\bm{\rho}_t}}_{1\times C}
\end{align}$$
定义初始状态 $ \delta_1[i_1]=k\big(z_1=i_1,\bm{X}\big)=\pi[i_1]$,同时我们注意到 $\displaystyle i_t$是可以任意的,递归计算我们得到一个网格图 trellis diagram。
$$\begin{align}
\Delta=\{\bm{\delta}_1,\cdots,\bm{\delta}_t,\cdots,\bm{\delta}_T\}
\end{align}$$
4.3、后向回溯
经过前向计算我们得到了最大的权重
$$\begin{align}
\max_{\mathcal{D}_t^z}g\big(\mathcal{D}_t^z,\mathcal{D}_t^\bm{x}\big)
=\max_{i_t}\delta_t[i_t]
=\max_{i_t}\max_{i_{t-1}}\max_{\cdots}\max_{i_2}\max_{i_2}\max_{i_1}\pi[i_1]
\prod_{t=2}^TA[i_{t-1},i_t]\rho_t[i_t]
\end{align}$$
求最佳隐数据集本质是网格图 trellis diagram $\displaystyle \Delta=\{\bm{\delta}_1,\cdots,\bm{\delta}_t,\cdots,\bm{\delta}_T\}$上搜索最短距离。为了解决这个问题,回顾动态规划思想:最优路径 $ \widehat{\mathcal{D}}_{1:T}^z$的一部分 $ \widehat{\mathcal{D}}_{t:T}^z$对于 $ t:T$的所有可能路径 $ \mathcal{D}_{t:T}^z$必然是最优。如果存在另外一条路径 $ \tilde{\mathcal{D}}_{t:T}^z$是最优的,那么会出现矛盾 $ \widehat{\mathcal{D}}_{1:t}^z\cup \tilde{\mathcal{D}}_{t:T}^z\neq \widehat{\mathcal{D}}_{1:T}^z $,所以 $ \widehat{\mathcal{D}}_{t:T}^z$ 必须是最优的。根据这一思想,我们定义回溯操作 traceback : $ \omega_t[\cdot]$,来从后向前还原最优状态序列。
$$\begin{align}
\widehat{z}_{t-1}
=\omega_t[z_t=i_t]
=\omega_t[i_t]
=\mathop{\mathrm{argmax}}_{i_{t-1}}\,\delta_{t-1}[i_{t-1}]A[i_{t-1},i_t] \rho_t[i_t]
\end{align}$$
定义 $ T$时刻最优状态 $\displaystyle \widehat{z}_{T}=\mathop{\mathrm{argmax}}_{i_T}\,\delta_T[i_T]$。应用回溯操作,得到最优路径:
$$\begin{align}
\widehat{\mathcal{D}}_{T}^z=\{\widehat{z}_{T}=\mathop{\mathrm{argmax}}_{i_T}\,\delta_T[i_T]\}\cup\{\widehat{z}_{t-1}=\omega_t[\hat{z}_{t}]\}_{t=T}^1
\end{align}$$
为了解决数据下溢问题,我们可以取对数
$$\begin{align}
&\ln\delta_{t}[i_t]
=\max_{i_{t-1}}\big[\ln\rho_t[i_t]+\ln A[i_{t-1},i_t]+\ln\delta_{t-1}[i_{t-1}]\big]\\
&\hat{z}_{t-1}=\omega_t[i_t]=\mathop{\mathrm{argmax}}_{i_{t-1}}\,\big[\ln\rho_t[i_t]+\ln A[i_{t-1},i_t]+\ln\delta_{t-1}[i_{t-1}]\big]
\end{align}$$
算法:维特比算法
1 $\displaystyle \bm{\delta}_1=\bm{\pi}$
2 $\displaystyle \text{ for }\,t=2:T$
$\displaystyle
\quad\begin{array}{|lc}
\text{ for }\,i_{t}=1:C \\
\quad\begin{array}{|lc}
\displaystyle \text{Traceback_Data}=\big[\ln\delta_t[i_t],\omega_{t-1}[i_t]\big]=\big[\mathop{\mathrm{colmax}}[\ln\bm{\delta}_{t-1}+\ln\bm{A}\big]^\text{T}+\ln\bm{\rho}_t
\end{array}\\
\text{ end}\\
\end{array}
$
3 end
$\displaystyle [\ln\delta_T,\hat{z}_{T}]=\max_{i_T}\,\ln\bm{\delta}_T$
4 $\displaystyle \text{ for }\,t=T:2$
$\displaystyle
\quad\begin{array}{|lc}
\hat{z}_{t-1}=\omega_{t}[\hat{z}_{t}]
\end{array}
$
5 end
6 $\displaystyle \hat{\bm{z}}$
五、条件随机场的训练
5.1、数据集的对数似然函数
$$\begin{align}
p\big(\bm{z}\mid\bm{X}\big)
&=p\big(\mathcal{D}^{\cdot|\cdot}_T\big)
=p\big(\mathcal{D}_T^z\mid\mathcal{D}_T^\bm{x}\big)
=\frac{1}{Z\big(\bm{X}\big)}\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)\prod_{t=1}^Tk\big(z_t,\bm{X}\big)\\
&=\frac{1}{Z\big(\bm{X}\big)}k\big(z_1,\bm{X}\big)\prod_{t=2}^Ts\big(z_{t-1},z_t,\bm{X}\big)k\big(z_t,\bm{X}\big)\\
\end{align}$$
定义整体数据集 $\displaystyle \mathcal{D}=\{\mathcal{[D}_T^z\mid \mathcal{D}_T^\bm{x}]_i\}_{i=1}^n$,含义是很清楚的:如果是句子的序列标注,就是 $\displaystyle n$带标注的句子。其中标注就是隐变量数据集,句子就是观测变量数据集。多个带标注的句子就是我们的 $\displaystyle \mathcal{D}$。
$$\begin{align}
\ln p\big(\mathcal{D}\big)
&=\ln \prod_{i=1}^np\big([\mathcal{D}_T^z\mid \mathcal{D}_T^\bm{x}]_i\big)
=\sum_{i=1}^n\ln p\big([\mathcal{D}_T^z\mid \mathcal{D}_T^\bm{x}]_i\big)\\
&=\sum_{i=1}^n\Bigg[\ln k\big(z_{1,i},\bm{X}_i\big)+\sum_{t=2}^T\bigg[\ln s\big(z_{t-1,i},z_{t,i},\bm{X}_i\big)+\ln k\big(z_{t,i},\bm{X}_i\big)\bigg]-\ln Z\big(\bm{X}_i\big)\Bigg]\\
&=\sum_{i=1}^n\ln k\big(z_{1,i},\bm{X}_i\big)+\sum_{i=1}^n\sum_{t=2}^T\bigg[\ln s\big(z_{t-1,i},z_{t,i},\bm{X}_i\big)+\ln k\big(z_{t,i},\bm{X}_i\big)\bigg]-\sum_{i=1}^n\ln Z\big(\bm{X}_i\big)\\
&=\sum_{i=1}^n\sum_{t=1}^T\ln k\big(z_{t,i},\bm{X}_i\big)+\sum_{i=1}^n\sum_{t=2}^T\ln s\big(z_{t-1,i},z_{t,i},\bm{X}_i\big)-\sum_{i=1}^n\ln Z\big(\bm{X}_i\big)\\
&=\sum_{i=1}^n\ln g\big(\bm{z}_{i},\bm{X}_{i}\big)-\sum_{i=1}^n\ln Z\big(\bm{X}_i\big)\\
\end{align}$$
我们必须清晰定义函数 $\displaystyle s,k$才能使得求导变得显然(注意转置 $\displaystyle \mathrm{T}$与下标 $\displaystyle T$)的区别,同时注意 $\displaystyle i$表示的是隐变量的状态。这样发射分数 $\displaystyle k(\cdot)$和转换分数函数 $\displaystyle s(\cdot)$就是类似于分类分布和矩阵分类分布的形势,如下:
$$\begin{align}
k\big(z_t=i,\bm{X}\big)&=\pi_{tc}^{\mathbb{I}(z_t=i)}\\
s\big(z_{t-1}=i,z_t=j,\bm{X}\big)&=A[i,j]^{\mathbb{I}(z_{t-1}=i)\mathbb{I}(z_t=j)}
\end{align}$$
为了更加简洁,我们重新定义隐变量 $\displaystyle z_t\in \mathcal{Z}=\{1,\cdots,C\}$的表现形式。我们使用 $\displaystyle 0-1$编码对隐边重新定义: $\displaystyle \bm{z}_t\in \mathcal{Z}=\{0,1\}^C$
$$\begin{align}
\bm{z}_t=[ 0\cdots1\cdots0 ]^\text{T}\iff \bm{z}_t[i]=z_{ti}=1\iff z_t=i
\end{align}$$
同时我们定义 $\displaystyle \bm{Z}_{T\times C}=[\bm{z}_1,\cdots,\bm{z}_t,\cdots,\bm{z}_T]^T$、$\displaystyle [\bm{\pi}_t]_{C\times 1}=\big[\pi_{z_1=1},\cdots,\pi_{z_t=i},\cdots,\pi_{z_T=C}\big]^T$。还定义 $\displaystyle \bm{\Pi}_{C\times T}=[\bm{\pi}_1,\cdots,\bm{\pi}_T]$。需要注意的是我们对向量的定义默认是列向量,对数据集的矩阵定义已行就是一条数据、一列就是一个特征。相关参数的定义适应数据集矩阵定义。继续,这样有
$$\begin{align}
k\big(z_t=i,\bm{X}\big)&=\bm{I}^\mathrm{T}\big[\bm{z}_t\odot\bm{\pi}_t\big]\\
s\big(z_{t-1}=i,z_t=j,\bm{X}\big)&=\bm{I}^\mathrm{T}\big[\bm{z}_{t-1}\bm{z}_t\odot \bm{A}\big]\bm{I}
\end{align}$$
我们将注意力再次集中到似然函数:
$$\begin{align}
\ell\big(\mathcal{D}\big)
&=\ln p\big(\mathcal{D}\big)
=\sum_{i=1}^n\ln g\big(\bm{Z}_{i},\bm{X}_{i}\big)-\sum_{i=1}^n\ln Z\big(\bm{X}_{i}\big)\\
&=\sum_{i=1}^n\sum_{t=1}^T\bm{I}^\mathrm{T}\big[\bm{z}_{t,i}\odot\ln\bm{\pi}_t\big]
+\sum_{i=1}^n\sum_{t=2}^T\bm{I}^\mathrm{T}\big[\bm{z}_{t-1,i}\bm{z}_{t,i}^\mathrm{T}\odot\ln\bm{A}\big]\bm{I}-\sum_{i=1}^n\ln Z\big(\bm{X_i}\big)\\
&=\sum_{i=1}^n\bm{I}^\mathrm{T}\big[\bm{Z}^\mathrm{T}\odot\ln\bm{\Pi}\big]\bm{I}+\sum_{i=1}^n\sum_{t=2}^T\bm{I}^\mathrm{T}\big[\bm{z}_{t-1,i}\bm{z}_{t,i}^\mathrm{T}\odot\ln\bm{A}\big]\bm{I}-\sum_{i=1}^n\ln Z\big(\bm{X_i}\big)
\end{align}$$
其中
$\displaystyle \ln g\big(\bm{Z},\bm{X}\big)
=\bm{I}^\mathrm{T}\big[\bm{Z}^\mathrm{T}\odot\ln\bm{\Pi}\big]\bm{I}
+\sum_{t=2}^T\bm{I}^\mathrm{T}\big[\bm{z}_{t-1}\bm{z}_{t}^\mathrm{T}\odot\ln\bm{A}\big]\bm{I}$
$\displaystyle \ln Z\big(\bm{X}\big)
=\ln\sum_{\bm{Z}}g(\bm{Z}, \bm{X})
=\ln\sum_{\bm{Z}}\bigg[\bm{I}^\mathrm{T}\big[\bm{Z}^\mathrm{T}\odot\bm{\Pi}\big]\bm{I}
+\sum_{t=2}^T\bm{I}^\mathrm{T}\big[\bm{z}_{t-1}\bm{z}_{t}^\mathrm{T}\odot\bm{A}\big]\bm{I}\bigg]$
5.2、对数似然函数求导
于是对参数 $\displaystyle \bm{\theta}=\{\bm{\Pi},\bm{A}\}$求导有
$$\begin{align}
\frac{\partial \ell}{\partial \bm{\varXi}}
&=\frac{\sum_{i}^n \bm{Z}_i^\mathrm{T}}{\bm{\Pi}}-\sum_{i=1}^n\frac{\sum_{\bm{Z}\in \mathcal{Z}}\bm{Z}_i^\mathrm{T}}{Z\big(\bm{X}_i\big)}
=\frac{\sum_{i}^n \bm{Z}_i^\mathrm{T}}{\bm{\Pi}}-\frac{nC^{C-1}\bm{I}_{C\times T}}{\sum_{i=1}^nZ\big(\bm{X}_i\big)}
=\bm{0}\\
\frac{\partial \ell}{\partial \bm{A}}
&=\frac{\sum_{i}^n \bm{z}_{t-1,i}\bm{z}_{t,i}^\mathrm{T}}{\bm{A}}-\sum_{i=1}^n\frac{\sum_{\bm{Z}\in \mathcal{Z}}\bm{z}_{t-1,i}\bm{z}_{t,i}^\mathrm{T}}{Z\big(\bm{X}_i\big)}
=\frac{\bm{S}}{\bm{A}}-\frac{nC^{C-1}\bm{I}_{C\times C}}{\sum_{i}^nZ\big(\bm{X}_i\big)}=\bm{0}
\end{align}$$
求解我们有:
$$\begin{align}
\bm{\Pi}&=\frac{1}{nC^{C-1}}\sum_{i=1}^nZ\big(\bm{X}_i\big)\sum_{i}^n \bm{Z}_i^\mathrm{T}\\
\bm{A}&=\frac{1}{nC^{C-1}}\sum_{i=1}^nZ\big(\bm{X}_i\big)\bm{S}
\end{align}$$
我们来理解一下这个公式的含义,发射分数实际上就是整体数据集中序列状态(0-1编码向量)的加和然后取平均。转移分数也是整体数据序列转移状态(0-1编码矩阵)的加和然后取平均,最后它们都乘以了一个归一常数。到这里参数 $\displaystyle \bm{\pi}_t$似乎从天而降,我们来明细一下。令 $\displaystyle \dim[\bm{X}]=T\times F$。观测变量 $\displaystyle \bm{x}$有 $\displaystyle F$个特征维度。定义 $\displaystyle \bm{\pi}_t=\bm{W}^\mathrm{T}\bm{x}_t+\bm{\omega}$
于是又有
$$\begin{align}
\bm{\Pi}_{C\times T}=\bm{W}_{C\times F}\bm{X}_{T\times F}^{\mathrm{T}}+\bm{\omega}_{C\times 1}\odot \bm{I}_{C\times T}
=\bm{W}\bm{X}^{\mathrm{T}}+\bm{\varXi}
\end{align}$$
$$\begin{align}
\ell\big(\mathcal{D}\big)
&=\ln p\big(\mathcal{D}\big)
=\sum_{i=1}^n\ln g\big(\bm{Z}_{i},\bm{X}_{i}\big)-\sum_{i=1}^n\ln Z\big(\bm{X}_{i}\big)\\
&=\sum_{i=1}^n\bm{I}^\mathrm{T}\big[\bm{Z}^\mathrm{T}\odot\ln \big[\bm{W}\bm{X}^{\mathrm{T}}+\bm{\varXi}\big]\big]\bm{I}+\sum_{i=1}^n\sum_{t=2}^T\bm{I}^\mathrm{T}\big[\bm{z}_{t-1,i}\bm{z}_{t,i}^\mathrm{T}\odot\ln\bm{A}\big]\bm{I}-\sum_{i=1}^n\ln Z\big(\bm{X_i}\big)
\end{align}$$
表达式已经比较复杂,求解析解存在困难,这里我们一般用拟牛顿,或者其他各种优化方法求解。
六、总结
1、我们使用条件随机场定义条件概率 $\displaystyle p\big(\bm{z}\mid \bm{X}\big)$。我们是基于整体特征定义了观测变量与隐变量的关系 $\displaystyle k\big(z_t,\bm{X}\big)$,而不像隐马尔可夫模型那样 $\displaystyle p\big(\bm{x}_t\mid z_t\big)$。这大大利于充分利用观测序列的信息。而不是局部信息。
2、然后我们使用图模型的信念传播 Belife Propagation,先后使用前向后向算法和维比特算法,解决了求值和求隐状态的问题。
3、最后我们定义了特殊的发射分数函数,和转移分数函数,解析的求解了参数,获得了参数自觉的一些解释。
4、人类可以通过一些精巧的设计,来获取超乎直观想象结果,上帝似乎很惊异。
| 版权声明 |  |
| 由引线小白创作并维护的柠檬CC博客采用署名-非商业-禁止演绎4.0国际许可证。 本文首发于柠檬CC [ https://www.limoncc.com ] , 版权所有、侵权必究。 | |
| 本文永久链接 | httpss://www.limoncc.com/post/875b887a5e7e39e56eea929a72336d4e/ |
| 如果您需要引用本文,请参考: |
| 引线小白. (Mar. 12, 2017). 《条件随机场模型》[Blog post]. Retrieved from https://www.limoncc.com/post/875b887a5e7e39e56eea929a72336d4e |
| @online{limoncc-875b887a5e7e39e56eea929a72336d4e, title={条件随机场模型}, author={引线小白}, year={2017}, month={Mar}, date={12}, url={\url{https://www.limoncc.com/post/875b887a5e7e39e56eea929a72336d4e}}, } |