作者: 引线小白-本文永久链接:httpss://www.limoncc.com/post/c0a3be9c86b2b4cd/
知识共享许可协议: 本博客采用署名-非商业-禁止演绎4.0国际许可证
摘要: 本文意在理清大语言模型中的强化学习。若有错误,请大家指正。
关键词:大语言模型,reinforcement learing,强化学习
[TOC]
一、理论基础
1.1、数学符号
首先来熟悉一下数学符号
1、$s$: 状态(state)
2、$a$: 表示动作(action)
3、$r$: 表示奖励(reward), 奖励依赖当前状态、当前动作、未来状态。也就说 $\displaystyle r_t=R_t\left(s_t,a_t,s_{t+1}\right)$
4、$u$: 表示回报(return),它是奖励的折现累积: $\displaystyle u_t = \sum_{i=t}^n\gamma^{i-t}r_i$, 如不特殊说明,一般有小写表示值,大写表示函数或者随机变量。例如
$$\begin{align}
U_t = R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \gamma^3 R_{t+3} + \cdots
\end{align}$$
有时候也不加区分。请根据上下文自行判断
5、$\pi$: 策略(policy) 是指如何根据观测到的状态做出决策。随机策略函数是一个概率密度函数$\pi:\mathcal{S}\times \mathcal{A}\to [0,1]$ 记为 $\pi(a\mid s)$。对于策略函数的参数 $\bm{\theta}$,这样也记做 $\displaystyle \pi_{\bm{\theta}}(a\mid s)$, $\displaystyle \pi(a\mid s,\bm{\theta})$
价值函数是回报的期望,即未来期望获得的奖励之和。价值函数反应了现状的好坏,价值函数越大说明现状越有利,知道 $U_t$的随机性来自奖励 $\{R_i\}_{i\geqslant t}$,奖励 $R_t$的随机性来自 $S_t$、 $A_t$、 $S_{t+1}$。
6、动作价值函数(action-value function)
$$\begin{align}
Q_{\pi}(s_t,a_t) = \mathbb{E}_{\mathcal{S}_{t+1:},\mathcal{A}_{t+1:}}\left[U_t\mid S_t=s_t,A_t=a_t\right]
\end{align}$$
其中:
$\displaystyle \mathcal{S}_{t+1:}=\{S_{t+1},S_{t+2},\cdots\}$
$\displaystyle \mathcal{A}_{t+1:}=\{A_{t+1},A_{t+2},\cdots\}$
有时候也用下面简写表示,以节约符号:
$$\begin{align}
Q_{\pi}(s_t,a_t)
= \mathbb{E}_{t+1:}\left[u_t\mid s_t,a_t\right]
= \mathbb{E}_{\mathcal{S}_{t+1:},\mathcal{A}_{t+1:}}\left[U_t\mid s_t,a_t\right]
\end{align}$$
7、最优动作价值函数(optimal action-value function)
$$\begin{align}
Q_*(s_t,a_t)= \max_{\pi}Q_{\pi}(s_t,a_t) \qquad \forall s_t \in \mathcal{S}, a_t \in \mathcal{A}
\end{align}$$
含义就是有多种策略函数 $\pi$可供选择,选择最好的策略函数:
$$\begin{align}
\pi^* =\arg\max_{\pi}Q_\pi(s_t,a_t) \qquad \forall s_t \in \mathcal{S}, a_t \in \mathcal{A}
\end{align}$$
8、状态价值函数(sata-value function)
$$\begin{align}
V_{\pi}(s_t)
&= \mathbb{E}_{A_t\sim \pi(\cdot\mid s_t)}\left[Q_{\pi}\left(s_t,A_t\right)\right]\\
&= \sum_{a\in \mathcal{A}}\pi(a\mid s_t)\cdot Q_{\pi}(s_t,a)
\end{align}$$
也就是说
$$\begin{align}
V_{\pi}(s_t) = \mathbb{E}_{\mathcal{S}_{t+1:},\mathcal{A}_{t:}}\left[U_t\mid S_t=s_t\right]
\end{align}$$
9、$A_{\pi}(s_t,a_t)$: 优势函数(advantage function)
$$\begin{align}
A_{\pi}(s_t,a_t) = Q_{\pi}(s_t,a_t) - V_{\pi}(s_t)
\end{align}$$
优势函数是动作价值函数和状态价值函数之差。反应了动作相对于平均值的优势。
1.2、策略学习与策略梯度
策略学习的目标在于调整策略使得状态价值 $V_{\pi}(S)$的均值最大。目标函数是
$$\begin{align}
\mathcal{J}(\bm{\theta})
&= \mathbb{E}_{s\in \mathcal{S}}[V_{\pi}(s)]\\
&= \mathbb{E}_{\mathcal{S}_{t:},\mathcal{A}_{t:}}\left[U_t\right]
\end{align}$$
其中 $\bm{\theta}$是策略网络的参数。
说的明白点就是消除了状态和动作的 $\mathcal{S},\mathcal{A}$的随机性。求它们的期望。这样就只剩下 $\displaystyle \pi_{\bm{\theta}}$。最大化
$$\begin{align}
\max_{\bm{\theta}}\mathcal{J}(\bm{\theta})
\end{align}$$
然后有策略梯度定理:
$$\begin{align}
\frac{\partial \mathcal{J}(\bm{\theta})}{\partial \bm{\theta}}
= \frac{1-\gamma^n}{1-\gamma}\cdot \mathbb{E}_{s_t\sim \rho,a_t\sim \pi}\left[\frac{\partial \log\pi_{\bm{\theta}}\left(a_t\mid s_t\right)}{\partial \bm{\theta}}\cdot Q_{\pi}(s_t,a_t)\right]
\end{align}$$
通常会忽略 $\frac{1-\gamma^n}{1-\gamma}$,简写成
$$\begin{align}
\nabla_{\bm{\theta}} \mathcal{J}(\bm{\theta})
= \mathbb{E}_{s_t\sim \rho,a_t\sim \pi}\left[\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(a_t\mid s_t) \cdot Q_{\pi}(s_t,a_t) \right]
\end{align}$$
1.3、带基线的策略梯度定理
$$\begin{align}
\nabla_{\bm{\theta}} \mathcal{J}(\bm{\theta})
= \mathbb{E}_{s_t\sim \rho,a_t\sim \pi}\left[\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(a_t\mid s_t) \cdot \left(Q_{\pi}(s_t,a_t)-b\right)\right]
\end{align}$$
其中 $b$是任意函数,且不依赖 $a_t$, 要证明上述定理只需证明
$$\begin{align}
\mathbb{E}_{a_t\sim \pi}\left[\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(a_t\mid s_t)\cdot b\right] = 0
\end{align}$$
实际上有 $b$不依赖于 $a_t$可以把 $b$提取到期望外面
$$\begin{align}
\mathbb{E}_{a_t\sim \pi}\left[\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(a_t\mid s_t)\cdot b\right]
&= b\cdot \mathbb{E}_{a_t\sim \pi}\left[\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(a_t\mid s_t)\right] \\
&=b\cdot \sum_{a_t\in \mathcal{A}}\big[\pi_{\bm{\theta}}(a_t\mid s_t)\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(a_t\mid s_t)\big]\\
&=b\cdot \sum_{a_t\in \mathcal{A}}\bigg[\pi_{\bm{\theta}}(a_t\mid s_t)\cdot\frac{1}{\pi_{\bm{\theta}}(a_t\mid s_t)}\cdot\frac{\partial \pi_{\bm{\theta}}(a_t\mid s_t)}{\partial \bm{\theta}}\bigg]\\
&=b\cdot \sum_{a_t\in \mathcal{A}}\bigg[\frac{\partial \pi_{\bm{\theta}}(a_t\mid s_t)}{\partial \bm{\theta}}\bigg] \\
& = b\cdot \frac{\partial }{\partial \bm{\theta}}\sum_{a_t\in \mathcal{A}}\pi_{\bm{\theta}}(a_t\mid s_t)\\
& = b\cdot \frac{\partial 1}{\partial \bm{\theta}}\\
& =0
\end{align}$$
这就证明了定理。不妨设 $\displaystyle b=V_{\pi}(s_t)$,这样有策略梯度
$$\begin{align}
\nabla_{\bm{\theta}} \mathcal{J}(\bm{\theta})
= \mathbb{E}_{s_t\sim \rho,a_t\sim \pi}\left[\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(a_t\mid s_t) \cdot \left(Q_{\pi}(s_t,a_t)-V_{\pi}(s_t)\right)\right]
\end{align}$$
而 $Q_{\pi}(s_t,a_t)-V_{\pi}(s_t)$实际上是优势函数 $A_{\pi}(s_t,a_t)$,这样有如下策略梯度
$$\begin{align}
\nabla_{\bm{\theta}} \mathcal{J}(\bm{\theta})
= \mathbb{E}_{s_t\sim \rho,a_t\sim \pi}\Big[\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(a_t\mid s_t) \cdot A_{\pi}(s_t,a_t)\Big]
\end{align}$$
这个策略梯度是各类RLHF(PPO,DPO,GRPO)的基础。当然看到这里好事者可能会问,为什么要引入优势函数,策略梯度定理如何证明等。那这里笔者就提示一下:
1、策略梯度定理证明稍微复杂,且证明技巧于实际应用比较远。笔者会在附录中介绍。
2、引入优势函数是减小方差、加速收敛。当然还有其他优点,这些笔者在后面会慢慢细说
最后笔者说说自己的心得,在这个技术高度集成的年代,理论前沿和应用前沿大多依赖很多底层基础知识。有些是应该弄明白的,对继续探索和实践是有益的。例如强化学习基础知识和策略梯度定理。但是有些其实可以放一放,没有必要深究。如策略梯度定理的证明,这就犹如神经网络的万能近似定理的证明,其实对你继续探索和实践深度学习影响甚微。此时如不能抑制自己的好奇心,非要搞清楚,你将会浪费大量时间和精力在非核心问题上。所以请记住适当抑制好奇心,才能走的更远。
1.4、GAE广义优势估计与价值网络学习
这节我们将讨论使用GAE广义优势估计[^2]来计算优势函数, $A_{\pi}(s_t,a_t) = Q_{\pi}(s_t,a_t) - V_{\pi}(s_t) $ 并于价值网络学习联系起来。
回顾一下动作价值函数的贝尔曼方程
$$\begin{align}
Q_{\pi}(a_t\mid s_t)=\mathbb{E}_{S_{t+1}\sim \rho}\bigg[R_t+\gamma V_{\pi}(S_{t+1})\mid S_t=s_t,A_t=a_t\bigg]
\end{align}$$
那么有
$$\begin{align}
A_{\pi}(s_t,a_t) = \mathbb{E}_{S_{t+1}\sim \rho}\bigg[R_t+\gamma V_{\pi}(S_{t+1})\mid S_t=s_t,A_t=a_t\bigg] - V_{\pi}(s_t)
\end{align}$$
给定状态 $s_t$,智能体执行动作 $a_t$,环境会给出奖励 $r_t$和新的状态 $s_{t+1}$, 用观测到的 $r_t$、 $s_{t+1}$对期望做蒙特卡洛近似, 并用价值网络 $v_{\bm{w}}(s_t)$替换价值函数 $V_{\pi}(s_t)$,这样有优势函数的估计值:
$$\begin{align}
\hat{A}_{\pi}(s_t,a_t)=r_t + \gamma v_{\bm{w}}(s_{t+1})-v_{\bm{w}}(s_t)
\end{align}$$
下面将目光注意到如何学习价值网络$v_{\bm{w}}(s_t)$,对状态价值函数有贝尔曼方程:
$$\begin{align}
V_{\pi}(s_t) = \mathbb{E}_{A_t\sim \pi}\bigg[\mathbb{E}_{S_{t+1}\sim \rho}\bigg[R_t+\gamma V_{\pi}(S_{t+1})\bigg]\bigg]
\end{align}$$
同样对期望做近似,具体就是在叙述一遍:给定状态 $s_t$,智能体执行动作 $a_t$,环境会给出奖励 $r_t$和新的状态 $s_{t+1}$, 用观测到的 $r_t$、 $s_{t+1}$对期望做蒙特卡洛近似, 并用价值网络 $v_{\bm{w}}(s_t)$替换价值函数 $V_{\pi}(s_t)$,这样有价值函数的估计值:
$$\begin{align}
\mathrm{\text{TD_Target}}_{k=1}:= \hat{y}_t = r_t + \gamma v_{\bm{w}}(s_{t+1})
\end{align}$$
又叫一步时间差分目标。如果对强化学习不熟悉,可能对反复出现的贝尔曼方程、TD(temporal difference,时间差分)等概念不太熟悉,这里稍微做点解释。希望给没有强化学习背景的同学减少一点困恼。
1、 $v_{\bm{w}}(s_t)$是价值网络值时刻 $t$做出的预测,其他没有任何事实成分
2、对于上式的一步时间差分目标是价值网络在时刻 $t+1$做出的预测,它部分基于真实观测的奖励 $r_t$。$\hat{y}_t$和 $v_{\bm{w}}(s_t)$都是对状态价值函数的估计,但 $\hat{y}_t$是部分基于事实的,因此比 $v_{\bm{w}}(s_t)$更加可信,应该鼓励 $v_{\bm{w}}(s_t)$接近 $\hat{y}_t$, 这样可以定义损失函数
$$\begin{align}
\ell(\bm{w}) = \frac{1}{2}\bigg[\hat{y}_t-v_{\bm{w}}(s_t)\bigg]^2
\end{align}$$
有梯度
$$\begin{align}
\nabla_{\bm{w}}\ell(\bm{w}) = \big[\underbrace{\hat{y}_t-v_{\bm{w}}(s_t)}_{\text{TD_Error}:\delta_t}\big]\nabla_{\bm{w}}v_{\bm{w}}(s_t)
\end{align}$$
称 $\hat{y}_t-v_{\bm{w}}(s_t)$为TD误差,或者叫时刻 $t$的一步时间差分误差 $\delta_t$:
$$\begin{align}
\mathrm{\text{TD_Error}}_{k=1}=\delta_t = \hat{y}_t-v_{\bm{w}}(s_t) = r_t + \gamma v_{\bm{w}}(s_{t+1}) - v_{\bm{w}}(s_t)
\end{align}$$
可以看到TD误差其实和优势函数的估计是一样的,对于多步时间差分误差,也会有多步优势函数估计:
$$\begin{align}
\hat{A}(k=1)=\mathrm{\text{TD_Error}}_{k=1}
&= r_t + \gamma v_{\bm{w}}(s_{t+1}) - v_{\bm{w}}(s_t)
= \delta_t\\
\hat{A}(k=2)=\mathrm{\text{TD_Error}}_{k=2}
&= r_t + \gamma \bigg[r_{t+1} + \gamma v_{\bm{w}}(s_{t+2})\bigg] - v_{\bm{w}}(s_t)\\
&= r_t + \gamma v_{\bm{w}}(s_{t+1}) - v_{\bm{w}}(s_t) + \gamma \bigg[r_{t+1} + \gamma v_{\bm{w}}(s_{t+2}) - v_{\bm{w}}(s_{t+1})\bigg] \\
&= \delta_t + \gamma \delta_{t+1}\\
\hat{A}(k=3)=\mathrm{\text{TD_Error}}_{k=3}
&= \delta_t + \gamma \delta_{t+1} + \gamma^2 \delta_{t+2}\\
&\vdots\\
\hat{A}(k)=\mathrm{\text{TD_Error}}_{k}
&= \sum_{i=1}^{k}\gamma^{i-1}\delta_{t+i-1}\\
&\vdots\\
\hat{A}(k=\infty)=\mathrm{\text{TD_Error}}_{\infty}
&= \sum_{i=1}^{\infty}\gamma^{i-1}\delta_{t+i-1}
\end{align}$$
所谓多步TD误差其实就是尽可能用多步观测到的值去估计价值函数。从而可以降低估计的偏差和误差。通常为了平衡偏差和误差,会引入一个超参数 $\lambda\in [0,1]$, 令
$$\begin{align}
\hat{A}_t(k)=\mathrm{\text{TD_Error}}_{k}
&= \sum_{i=1}^{k}\big(\gamma\lambda\big)^{i-1}\delta_{t+i-1}\\
&=\delta_t + \gamma\lambda\bigg[\delta_{t+1}+\big(\gamma\lambda\big)\delta_{t+2}+\cdots +\big(\gamma\lambda\big)^{k-2}\delta_{t+k-1} \bigg]\\
& = \delta_t + \gamma\lambda\hat{A}_{t+1}(k-1)
\end{align}$$
注意一下边界条件,当轨迹在 $T$时刻终止 后续状态价值为 $V_{\pi}(s_{T+1})=0$,在价值函数学习代码的实现中,一般会先递归计算优势函数估计。然后使用如下公式计算TD目标。
$$\begin{align}
\hat{y}_t=\mathrm{\text{TD}}_{k} = \hat{A}_t(k) + v_{\bm{w}}(s_t)
\end{align}$$
当然如果对概率论缺乏直觉的朋友,可能一下子无法理解这种做法为啥能平衡偏差和误差。思考如下问题:求一组随机变量和的均值,那么如果我观测到其中 $k$的随机变量的值,替换对应的随机变量求均值,那么均值的方差和偏差如何变化?,不妨设这组随机变量是独立同分布的高斯分布 $x_i\sim \mathcal{N}(\mu,\sigma^2)$, $s_n= \frac{1}{n}\sum_{i=1}^n x_i$
如果我们没有观测到任何值
$$\begin{align}
\mathbb{E}[s_n] = \mu,\mathrm{var}[s_n] = \frac{\sigma^2}{n}
\end{align}$$
如果观测到k组值,通常假设观测存在偏差 $\mathring{x}_i=\mu+\delta_i$
那么均值有
$$\begin{align}
\mathbb{E}[s_n] = \frac{1}{n}\big[\sum_i^k \mathring{x}_i +(n-k)\mu\big] = \mu+ \frac{\sum_i^k\delta_i}{n} \geqslant \mu
\end{align}$$
那么误差有
$$\begin{align}
\mathrm{var}[s_n] = \frac{(n-k)\sigma^2}{n^2} \leqslant \frac{\sigma^2}{n}
\end{align}$$
也就是说方差变小,偏差变大。如果我们给观测值加一个超参数 $\lambda\in [0,1]$,$\mathring{x}_i=\lambda\mu+\lambda\delta_i$, 来平衡偏差和误差
那么均值有
$$\begin{align}
\mathbb{E}[s_n](\lambda)
=\frac{1}{n}\big[\sum_i^k \mathring{x}_i +(n-k)\mu\big]
=\frac{n-k(1-\lambda)}{n}\mu+ \frac{\sum_i^k \lambda\delta_i}{n}
\leqslant \mu+ \frac{\sum_i^k\delta_i}{n}
\end{align}$$
相信通过这个例子,应该会有所感觉。
二、PPO近端策略优化
2.1、代理目标函数
网络上很多文章,写的多有错误,本文笔者将尽可能用清晰的数学符号,澄清各类问题。经过前期铺垫,终于可以谈论PPO了。为了使用自动微分,不太可能使用强化学习的原始目标函数 $\mathcal{J}(\bm{\theta}) = \mathbb{E}_{s\sim \rho}[V_{\pi}(s)]$, 因为需要对个步骤对状态和动作求积分或求和,这是非常困难的,这里引入了一个代理目标函数(surrogate objective),只要确保代理目标函数的梯度和原始目标函数一致即可。回顾一下策略梯度
$$\begin{align}
\nabla_{\bm{\theta}} \mathcal{J}(\bm{\theta})
= \mathbb{E}_{s_t\sim \rho,a_t\sim \pi}\Big[\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(a_t\mid s_t) \cdot A_{\pi}(s_t,a_t)\Big]
\end{align}$$
那么设定这样的代理目标函数是显而易见的:
$$\begin{align}
\mathcal{L}^{PG}(\bm{\theta}) = \mathbb{E}_{s_t\sim \rho,a_t\sim \pi}\Big[\log\pi_{\bm{\theta}}(a_t\mid s_t) \cdot A_{\pi}(s_t,a_t)\Big]
\end{align}$$
也就说可一灵活设计目标函数,只要确保该目标函数的梯度和策略梯度定理一致即可。这也是经常看到论文和文章中总是提及策略梯度定理原因。因为只要保证如下公式
$$\begin{align}
\nabla_{\bm{\theta}} \mathcal{L}^{PG}(\bm{\theta})
=\nabla_{\bm{\theta}} \mathcal{J}(\bm{\theta})
\end{align}$$
优化方向上就能在理论上保证和原始的强化学习目标是一致的。然后实践证明这个最明显的目标函数表现并不好。PPO论文[^3]使用了TRPO(trus region policy optimuization,置信域策略优化中提出的函数),回到原始目标函数
$$\begin{align}
\mathcal{J}(\bm{\theta})
&= \mathbb{E}_{s_t\sim \rho}[V_{\pi}(s_t)]\\
&= \mathbb{E}_{s_t\sim \rho}\bigg[\mathbb{E}_{a_t\sim \pi}\big[Q_{\pi}(s_t, a_t)\big]\bigg]\\
&= \mathbb{E}_{s_t\sim \rho}\bigg[\sum_{a_t\in \mathcal{A}}\pi_{\bm{\theta}}(a_t\mid s_t)\cdot Q_{\pi}(s_t, a_t)\bigg]\\
&= \mathbb{E}_{s_t\sim \rho}\bigg[\sum_{a_t\in \mathcal{A}}\pi_{\bm{\theta}_\text{old}}(a_t\mid s_t)\frac{\pi_{\bm{\theta}}(a_t\mid s_t)}{\pi_{\bm{\theta}_\text{old}}(a_t\mid s_t)}\cdot Q_{\pi}(s_t, a_t)\bigg]\\
& = \mathbb{E}_{s_t\sim \rho,a_t\sim \pi_{\bm{\theta}_\text{old}}}\bigg[\frac{\pi_{\bm{\theta}}(a_t\mid s_t)}{\pi_{\bm{\theta}_\text{old}}(a_t\mid s_t)}\cdot Q_{\pi}(s_t, a_t)\bigg]\\
\end{align}$$
这里变化为新旧策略比例的原因是为了纳入重要性采样的trick提高学习效率。如果不熟悉重要性采样的同学,请找本书看,这里推荐Sheldon M. Ross的《Simulation》。
使用优势函数$A_{\pi}(s_t,a_t) = Q_{\pi}(s_t,a_t) - V_{\pi}(s_t) $ ,在这个基础上PPO提出了裁剪版的代理目标函数
$$\begin{align}
\mathcal{L}^{\text{CLIP}}(\bm{\theta})
=\mathbb{E}_{s_t\sim \rho,a_t\sim \pi_{\bm{\theta}_\text{old}}}\bigg[\min\left[\frac{\pi_{\bm{\theta}}(a_t\mid s_t)}{\pi_{\bm{\theta}_\text{old}}(a_t\mid s_t)},\mathrm{\text{clip}}\left[\frac{\pi_{\bm{\theta}}(a_t\mid s_t)}{\pi_{\bm{\theta}_\text{old}}(a_t\mid s_t)},1-\epsilon,1+\epsilon\right]\right]\cdot A_{\pi}(s_t,a_t)\bigg]
\end{align}$$
其中令 $\displaystyle \eta_t(\bm{\theta})=\frac{\pi_{\bm{\theta}}(a_t\mid s_t)}{\pi_{\bm{\theta}_\text{old}}(a_t\mid s_t)}$
$$\begin{align}
\mathcal{L}^{\text{CLIP}}(\bm{\theta})
=\mathbb{E}_{s_t\sim \rho,a_t\sim \pi_{\bm{\theta}_\text{old}}}\bigg[\min\big[\eta_t(\bm{\theta}),\mathrm{\text{clip}}[\eta_t(\bm{\theta}),1-\epsilon,1+\epsilon]\big]\cdot A_{\pi}(s_t,a_t)\bigg]
\end{align}$$
用优势函数替代动作价值函数, 同时引入clip。有诸多的好处:
- 1、已经证明这个操作不会改变梯度的期望值,当通过减小 $Q_{\pi}(s_t,a_t)$的绝对波动幅度,降低了方差。
- 2、优势函数提供了更加明确的优化信号,因为优势函数衡量的是动作的相对好坏,使得策略更新方向更清晰,相比于使用动作价值函数,优势函数提供的梯度信号更稳定,减少了噪声干扰,从而加速收敛。
- 3、与广义优势估计(GAE)结合,通过多步TD残差的加权和计算优势函数的估计。GAE平衡了蒙特卡洛方法(低偏差、高方差)和单步TD方法(高偏差、低方差),进一步优化了方差-偏差权衡,提升收敛效率。
- 4、优势函数通过相对价值调整,而非依赖绝对回报,使得策略更新的幅度更加合理。结合PPO的裁剪机制(Clip机制),可限制策略更新的步长,避免因单次更新过大导致的策略崩溃。
- 5、优势函数结合GAE,充分利用多步回报信息,减少对单一轨迹片段的依赖。这使得算法在相同样本量下能提取更多有效信息,提升数据利用率。
- 6、优势函数指导策略优先选择高优势动作(利用),但PPO的熵正则项(Entropy Bonus)可保留一定随机性(探索)。两者结合避免了策略过早陷入局部最优。注意上面的公式,没有加入熵正则。
- 7、优势函数依赖状态价值函数的估计,这要求Critic网络准确预测状态价值。PPO通过联合优化策略网络(Actor)和价值网络(Critic),使两者相互促进:Critic为Actor提供低方差梯度,Actor生成的数据帮助Critic更准确估计价值。
- 8、在稀疏奖励任务中,绝对回报可能长期为零或变化微小,而优势函数通过比较动作的相对价值,仍能提供有效的梯度信号,帮助策略在早期阶段逐步改进。
2.2、大语言模型场景
上述分析都是在强化学习的状态动作场景。这里将转化为大模型场景。在LLM里,状态是每个token的之前的token。一般我们会从提示词或者问题 $q$出发,迭代输出每步动作,也就是token $o_t$
$$\begin{align}
\mathbb{E}_{s_t\sim \rho,a_t\sim \pi_{\bm{\theta}_\text{old}}}\to
\mathbb{E}_{q\sim \rho(Q),o_t\sim \pi_{\bm{\theta}_\text{old}}}
\end{align}$$
也就是说有问题对数据集 $\displaystyle \mathcal{D}=\{(q_i,o_1 \cdots o_{t_i})\}_{i=1}^n$
$$\begin{align}
\mathcal{L}^{\text{PPO}}(\bm{\theta})
&=\mathbb{E}_{q\sim \rho(Q),o_t\sim \pi_{\bm{\theta}_\text{old}}}\bigg[\min\left[\frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\text{old}}(o_t\mid q,o_{:t})},\mathrm{\text{clip}}\left[\frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\text{old}}(o_t\mid q,o_{:t})},1-\epsilon,1+\epsilon\right]\right]\cdot A_{\pi}(q,o_t)\bigg]
\end{align}$$
2.3、PPO中的KL散度
为减轻奖励模型的过度优化,PPO还会引入参考模型的 $\text{KL}$散度,在计算每个token奖励时,减去 $\{o_1,\cdots,o_t\}$上的散度,
$$\begin{align}
r_t=\pi_{\bm{\theta}_{\textit{rm}}}(q,o_{:t})-\beta \mathbb{KL}\big[\pi_{\bm{\theta}} ||\pi_{\bm{\theta}_\textit{ref}}\big]
\end{align}$$
其中
$\pi_{\bm{\theta}_{\textit{rm}}}$是奖励模型(reward model), $\displaystyle \mathbb{KL}\big[\pi_{\bm{\theta}} ||\pi_{\bm{\theta}_\textit{ref}}\big] = \log \frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\textit{ref}}(o_t\mid q,o_{:t})}$
在这个地方,肯定有人会问为啥是把这个所谓的KL在计算token奖励时加入,而不是基于正则的方式加入到损失函数或者目标函数里面:
$$\begin{align}
\mathcal{L}^{\text{PPO}}(\bm{\theta})
&=\mathbb{E}_{q\sim \rho,o_t\sim \pi_{\bm{\theta}_\text{old}}}\bigg[\min\left[\frac{\pi_{\bm{\theta}}(o_t,\mid q,o_{:t})}{\pi_{\bm{\theta}_\text{old}}(o_t\mid q,o_{:t})},\mathrm{\text{clip}}\left[\frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\text{old}}(o_t\mid q,o_{:t})},1-\epsilon,1+\epsilon\right]\right]\cdot A_{\pi}(q,o_t)\bigg]-\beta \mathbb{\hat{KL}}\big[\pi_{\bm{\theta}} ||\pi_{\bm{\theta}_\textit{ref}}\big]
\end{align}$$
这样才是更加常规做法。奈何GPT2,GPT3相关论文代码确实是这么写的,可以参考知乎上的讨论在强化学习 PPO 算法中,为什么可以把 KL 散度直接放进负奖励?
PPO技术要点差不多已经理清,这里再全局回顾一下:
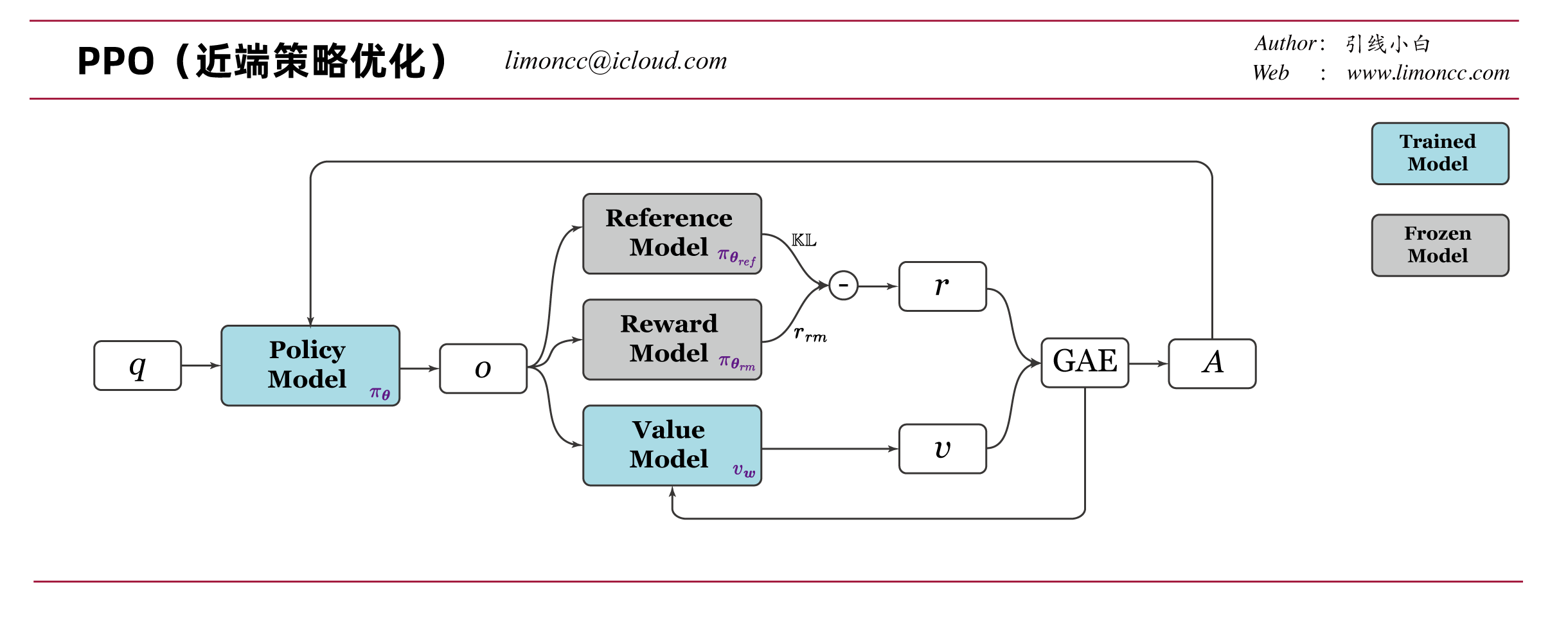
1、有两个可以训练的模型:策略模型 $\pi_{\bm{\theta}}$、 价值模型$v_{\bm{w}}$
2、有一已经训练好的奖励模型 $\pi_{\bm{\theta}_{\textit{rm}}}$
3、还有一个冻结参数的参考模型 $\pi_{\bm{\theta}_\textit{ref}}$
deepseek math的论文图画的很好,笔者略微修改一下,并添加注释,以便更加清晰理解:
三、GRPO组相对策略优化
3.1、GRPO的目标函数
注意到PPO中有四个模型,实属非常浪费资源。GRPO[^4]提出了更加节约资源的版本。对于PPO,deepseek math给出了更加明晰的公式, 适合照着公式写代码。明确加入了 $\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}$,对于一个问题 $q$的输出 $\bm{o}=[o_1,o_2,\cdots,o_t,\cdots,o_T]$, 明确了处理方式。之前的目标函数代码实现的时候默认如此,但是并没有显示的写出来。
$$\begin{align}
\mathcal{L}_{\textit{PPO}}(\bm{\theta})
&=\mathbb{E}_{q\sim \rho(Q),\bm{o}\sim \pi_{\bm{\theta}_\text{old}}}\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}\bigg[\min\left[\frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\text{old}}(o_t\mid q,o_{:t})},\mathrm{\text{clip}}\left[\frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\text{old}}(o_t\mid q,o_{:t})},1-\epsilon,1+\epsilon\right]\right]\cdot A_{\pi}(q,o_t)\bigg]
\end{align}$$
deepseek math论文提出了,GRPO组相对策略优化,目标函数是
$$\begin{align}
&\mathcal{L}_{\textit{GRPO}}(\bm{\theta})
=\mathbb{E}_{q\sim \rho(Q),\{\bm{o}_i\}_{i=1}^G\sim \pi_{\bm{\theta}_\text{old}}}\\
&\frac{1}{G}\sum_{i=1}^G\frac{1}{|\bm{o}_i|}\sum_{t=1}^{|\bm{o}_i|}
\bigg[\min\left[\frac{\pi_{\bm{\theta}}(o_{i,t}\mid q,o_{i,:t})}{\pi_{\bm{\theta}_\text{old}}(o_{i,t}\mid q,o_{i,:t})},\mathrm{\text{clip}}\left[\frac{\pi_{\bm{\theta}}(o_{i,t}\mid q,o_{i,:t})}{\pi_{\bm{\theta}_\text{old}}(o_{i,t}\mid q,o_{i,:t})},1-\epsilon,1+\epsilon\right]\right]\cdot A_{\pi}(q,o_{i,t})-\beta \mathbb{\hat{KL}}\big[\pi_{\bm{\theta}} ||\pi_{\bm{\theta}_\textit{ref}}\big]\bigg]
\end{align}$$
3.2、GRPO的KL散度
对于 $\text{KL}$散度的计算实际代码实现是通过蒙特卡洛估计来实现的,这也是为什么KL项在期望符号里面的原因。实际上这样的。
$$\begin{align}
\mathbb{\hat{KL}}\big[\pi_{\bm{\theta}} ||\pi_{\bm{\theta}_\textit{ref}}\big] =\frac{\pi_{\bm{\theta}_\textit{ref}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}- \log \frac{\pi_{\bm{\theta}_\textit{ref}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}-1
\end{align}$$
为何使用这个估计,这篇博文写了如何对KL散度做蒙特卡洛近似,能实现偏差与方差平衡:https://joschu.net/blog/kl-approx.html[^5],这里啰嗦几句。KL通常是基于分布整体来计算的:
$$\begin{align}
\mathbb{KL}\big[\pi_{\bm{\theta}} ||\pi_{\bm{\theta}_\textit{ref}}\big]
=\sum_{o_t \in \mathcal{Vocab}}\pi_{\bm{\theta}} \log \frac{\pi_{\bm{\theta}}}{\pi_{\bm{\theta}_\textit{ref}}}
\end{align}$$
这里笔者稍微做点解释,做蒙特卡洛模拟最简单就是使用 $\displaystyle \log \frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\textit{ref}}(o_t\mid q,o_{:t})}$来做估计。但是这个是估计的方差比较大。因为计算 $log(\cdot)$会出现负值,而 $\mathbb{KL}$是非负的。要减少方差需要添加一个与 $\log \frac{\pi_{\bm{\theta}}}{\pi_{\bm{\theta}_\textit{ref}}}$变化方向相反,且均值为零的量。 $\displaystyle \frac{\pi_{\bm{\theta}_\textit{ref}}}{\pi_{\bm{\theta}}}-1$似乎是一个不错的选择。而且 $\log(x)\leqslant x-1$,这样估计量 $\displaystyle \log \frac{\pi_{\bm{\theta}}}{\pi_{\bm{\theta}_\textit{ref}}}+\frac{\pi_{\bm{\theta}_\textit{ref}}}{\pi_{\bm{\theta}}}-1$始终是非负。具体可以参见博文中的关于Bregman距离的论述。
3.3、GRPO的优势函数
对于优势函数的估计体现了GRPO组相对策略优化这个名字的含义, 在GRPO中没有价值模型,而是使用同一个问题的一组输出数据 $\{\{q,\bm{o}_i\}\}_{i=1}^G$,来计算相对优势。
- 1、对于过程监督(process supervision),也就是说同一个问题 $q$个一组输出中的每个token的优势估计是这样计算的:
$$\begin{align}
\hat{A}_{i,t}=\hat{A}_{\pi}(q,o_{i,t}) = \frac{r(o_{i,t})-\text{mean}(\bm{R})}{\text{std}(\bm{R})}
\end{align}$$
其中 $\displaystyle \bm{R} = \{\{r(o_{1,1}),\cdots r(o_{1,t})\}_1,\cdots,\{r(o_{i,1}),\cdots r(o_{i,t})\}_i,\cdots,\{r(o_{G,1}),\cdots r(o_{G,t})\}_G\}$
- 2、对于结果监督(outcome supervison)有, 也就是说同一个问题 $q$个的一个输出中的每个token的优势估计相同的:
$$\begin{align}
\hat{A}_{i,t}=\hat{A}_{\pi}(q,\bm{o}_{i}) = \frac{r(\bm{o}_{i})-\text{mean}(\bm{R})}{\text{std}(\bm{R})}
\end{align}$$
其中 $\displaystyle \bm{R} = \{r(\bm{o}_1),\cdots,r(\bm{o}_i),\cdots,r(\bm{o}_G)\}$
3.4、deepseek R1模型的目标函数
deepseek R1模型的目标函数[^1]和deepseek math中的目标函数稍微不太一样。deepseek的思维链模型,没有使用过程奖励。目标函数中可以看到是整体计算整个输出求平均。而且R1除了没有价值模型,还没有奖励模型。奖励的计算基于规则、代码验证器、格式验证来计算的。这大大节约了资源,也减少了学习难度。
$$\begin{align}
&\mathcal{L}_{\textit{GRPO}}(\bm{\theta})
=\mathbb{E}_{q\sim \rho(Q),\{\bm{o}_i\}_{i=1}^G\sim \pi_{\bm{\theta}_\text{old}}}\\
&\frac{1}{G}\sum_{i=1}^G
\frac{1}{|\bm{o}_i|}\sum_{t=1}^{\bm{|\bm{o}_i|}}
\bigg[\min\left[\frac{\pi_{\bm{\theta}}(o_{i,t}\mid q,o_{i,:t})}{\pi_{\bm{\theta}_\text{old}}(o_{i,t}\mid q,o_{i,:t})},\mathrm{\text{clip}}\left[\frac{\pi_{\bm{\theta}}(o_{i,t}\mid q,o_{i,:t})}{\pi_{\bm{\theta}_\text{old}}(o_{i,t}\mid q,o_{i,:t})},1-\epsilon,1+\epsilon\right]\right]\cdot A_{\pi}(q,\bm{o}_i)-\beta \mathbb{\hat{KL}}\big[\pi_{\bm{\theta}} ||\pi_{\bm{\theta}_\textit{ref}}\big]\bigg]
\end{align}$$
其中
$\displaystyle \hat{A}_{i,t}=\hat{A}_{\pi}(q,\bm{o}_{i}) = \frac{r(\bm{o}_{i})-\text{mean}(\bm{R})}{\text{std}(\bm{R})}$
$\displaystyle \mathbb{\hat{KL}}\big[\pi_{\bm{\theta}} ||\pi_{\bm{\theta}_\textit{ref}}\big]
=\frac{\pi_{\bm{\theta}_\textit{ref}}(o_{i,t}\mid q,o_{i,:t})}{\pi_{\bm{\theta}}(o_{i,t}\mid q,o_{i,:t})}- \log \frac{\pi_{\bm{\theta}_\textit{ref}}(o_{i,t}\mid q,o_{i,:t})}{\pi_{\bm{\theta}}(o_{i,t}\mid q,o_{i,:t})}-1$
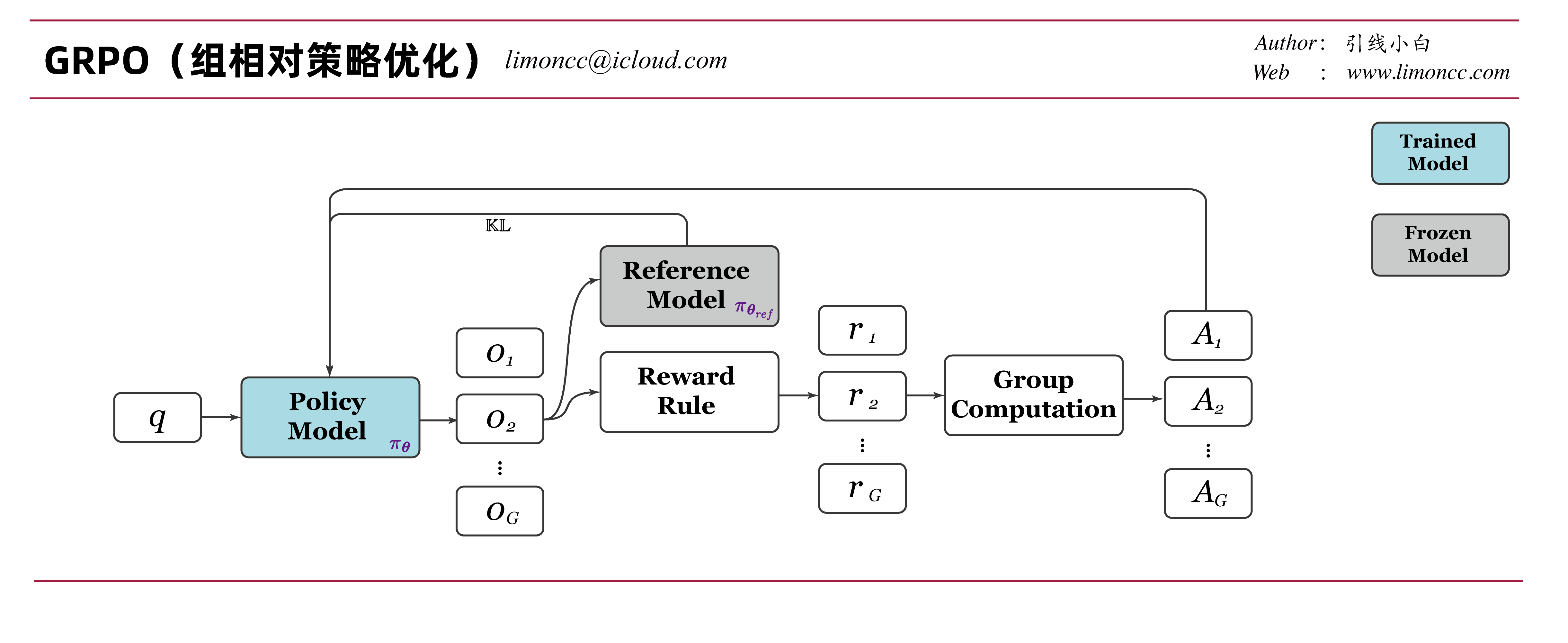
R1的训练流程经过了三个阶段,下面是笔者绘制的流程图,并标注了关键节点的一些注意要点。注意在最后阶段其实是有奖励模型参与的。第三阶段的生成600k的推理数据在使用拒绝采样时也使用了奖励模型。注意在deepseekv3的奖励模型中是同时输出奖励理由的思维链和奖励分数的。
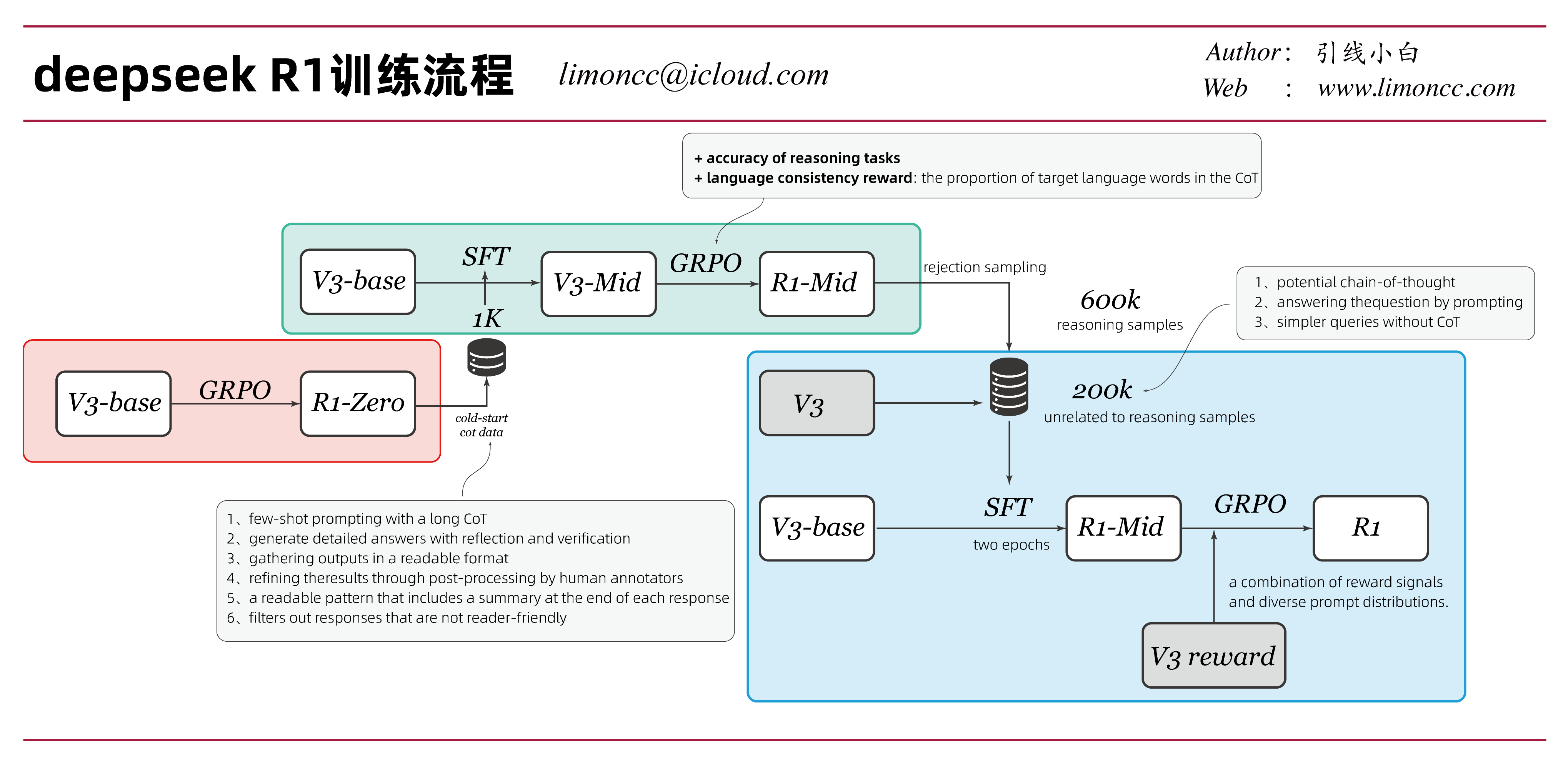
四、大语言模型中强化学习的统一范式
deepseek math论文中对各类RLHF(SFT、RFT、DPO、PPO、GRPO)提出了一个统一强化学习框架,下面是统一的策略梯度公式:
$$\begin{align}
\nabla_{\bm{\theta}}\mathcal{J}_{\mathcal{\textcolor{red}{A}}}
=\underbrace{\mathbb{E}_{(q,o)\sim \textcolor{red}{\mathcal{D}}}}_{\textit{Data Source}}
\Bigg[\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}\underbrace{\textit{GC}_{\mathcal{A}}(q,o,r,\textcolor{red}{\pi_{\bm{\theta}_\textit{rm}}}}_{\textit{Gradient Coefficient}})\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(o_t\mid q,o_{:t})\Bigg]
\end{align}$$
有三个关键组件
1、 Data Source $\mathcal{D}$ 它决定了训练数据
2、 Reward Function $\pi_{\bm{\theta}_\textit{rm}}$ 它是训练奖励信号的来源
3、 Algorithm $\mathcal{A}$ 它处理了训练数据和梯度系数(Gradient Coefficient)中的奖励信号,生成决定数据的惩罚项或强化幅度。
下面来一一考察:
4.1、SFT
监督微调(Supervised Fine-tuning)
目标函数
$$\begin{align}
\mathcal{L}_{\textit{SFT}}(\bm{\theta})
=\mathbb{E}_{q,\bm{o}\sim \rho(Q,O)}
\bigg[\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}\log\pi_{\bm{\theta}}(o_t\mid q,o_{:t})\bigg]
\end{align}$$数据集
在问题对数据集中抽样, 其中 $q$是问题, $\bm{o}=[o_1,\cdots,o_{|\bm{o}|}]$是回答的每个token。
$$\begin{align}
\mathcal{D}=\{(q_i,\bm{o}_i)\}_{i=1}^n
\end{align}$$
梯度
$$\begin{align}
\nabla_{\bm{\theta}}\mathcal{L}_{\textit{SFT}}(\bm{\theta})
=\mathbb{E}_{q,\bm{o}\sim \rho(Q,O)}
\bigg[\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(o_t\mid q,o_{:t})\bigg]
\end{align}$$奖励函数
$$\begin{align}
\pi_{\bm{\theta}_\textit{rm}}=1
\end{align}$$梯度系数
$$\begin{align}
\textit{GC}_{\textit{SFT}}(q,o,r,\pi_{\bm{\theta}_\textit{rm}})=1
\end{align}$$
4.2、RFT
决绝采样微调(Rejection Sampling Fine-tuning)
目标函数
$$\begin{align}
\mathcal{L}_{\textit{RFT}}(\bm{\theta})
=\mathbb{E}_{q\sim \rho(Q),\bm{o}\sim \pi_{\textit{sft}}}
\bigg[\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}
\mathbb{I}(\bm{o})
\log\pi_{\bm{\theta}}(o_t\mid q,o_{:t})\bigg]
\end{align}$$数据集
RFT是在已经训练好的SFT模型 $ \pi_{\textit{sft}}$上, 对问题 $q$生成多个回答,并标注正确和错误的回答。$\bm{o}=[o_1,\cdots,o_{|\bm{o}|}]$是回答的每个token。
$$\begin{align}
\mathcal{D}=\{(q_i,\bm{o}_i^{True}\,or\,\bm{o}_i^{False})\}_{i=1}^n
\end{align}$$
- 梯度
$$\begin{align}
\nabla_{\bm{\theta}}\mathcal{L}_{\textit{RFT}}(\bm{\theta})
=\mathbb{E}_{q\sim \rho(Q),\bm{o}\sim \pi_{\textit{sft}}}
\bigg[\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}
\mathbb{I}(\bm{o})
\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(o_t\mid q,o_{:t})\bigg]
\end{align}$$
奖励函数
$$\begin{align}
\pi_{\bm{\theta}_\textit{rm}}=1
\end{align}$$梯度系数
$$\begin{align}
\textit{GC}_{\textit{RFT}}(q,o,r,\pi_{\bm{\theta}_\textit{rm}})=\mathbb{I}(\bm{o})=\begin{cases}1&\text{if } \bm{o}=True\\0&\text{if } \bm{o}=False \end{cases}
\end{align}$$
4.3、Online RFT
在线决绝采样微调(Online Rejection Sampling Fine-tuning)和RFT的区别,在于数据会通过实时策略模型 $\pi_{\bm{\theta}}$生成。而不是离线已经训练好的 $\pi_{\textit{sft}}$模型。
- 目标函数
$$\begin{align}
\mathcal{L}_{\textit{OnRFT}}(\bm{\theta})
=\mathbb{E}_{q\sim \rho(Q),\bm{o}\sim \pi_{\bm{\theta}}}
\bigg[\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}
\mathbb{I}(\bm{o})
\log\pi_{\bm{\theta}}(o_t\mid q,o_{:t})\bigg]
\end{align}$$
4.4、DPO
直接偏好优化(Direct Preference Optimization)
目标函数
$$\begin{align}
\mathcal{L}_{\textit{DPO}}(\bm{\theta})
=\mathbb{E}_{q\sim \rho(Q),\bm{o}^{+},\bm{o}^{-}\sim \pi_{\textit{sft}}}\left[
\log\sigma\bigg(
\beta\frac{1}{|\bm{o}^+|}\sum_{t=1}^{|\bm{o}^+|}
\log \frac{\pi_{\bm{\theta}}(o_t^+\mid q,o_{:t}^+)}{\pi_{\bm{\theta}_\textit{ref}}(o_t^+\mid q,o_{:t}^+)}
-\beta\frac{1}{|\bm{o}^-|}\sum_{t=1}^{|\bm{o}^-|}
\log \frac{\pi_{\bm{\theta}}(o_t^-\mid q,o_{:t}^-)}{\pi_{\bm{\theta}_\textit{ref}}(o_t^-\mid q,o_{:t}^-)}
\bigg)
\right]
\end{align}$$数据集
DPO是是问题 $q$上的偏好数据,并标注接受回答 $+$和拒绝回答 $-$。$\bm{o}=[o_1,\cdots,o_{|\bm{o}|}]$是回答的每个token。
$$\begin{align}
\mathcal{D}=\{(q_i,\bm{o}_i^{+}\,or\,\bm{o}_i^{-})\}_{i=1}^n
\end{align}$$
- 梯度
$$\begin{align}
\nabla_{\bm{\theta}}\mathcal{L}_{\textit{DPO}}(\bm{\theta})
=\mathbb{E}_{q\sim \rho(Q),\bm{o}^{+},\bm{o}^{-}\sim \pi_{\textit{sft}}}\left[
\beta\cdot\textit{GC}_{\textit{DPO}}(q,o,t)\bigg(
\frac{1}{|\bm{o}^+|}\sum_{t=1}^{|\bm{o}^+|}
\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(o_t^+\mid q,o_{:t}^+)
-\frac{1}{|\bm{o}^-|}\sum_{t=1}^{|\bm{o}^-|}
\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(o_t^-\mid q,o_{:t}^-)
\bigg)
\right]
\end{align}$$
奖励函数
$$\begin{align}
\pi_{\bm{\theta}_\textit{rm}}=1
\end{align}$$梯度系数
$$\begin{align}
\textit{GC}_{\textit{DPO}}(q,o,t)
=\sigma\bigg(
\beta
\log \frac{\pi_{\bm{\theta}}(o_t^+\mid q,o_{:t}^+)}{\pi_{\bm{\theta}_\textit{ref}}(o_t^+\mid q,o_{:t}^+)}
-\beta
\log \frac{\pi_{\bm{\theta}}(o_t^-\mid q,o_{:t}^-)}{\pi_{\bm{\theta}_\textit{ref}}(o_t^-\mid q,o_{:t}^-)}
\bigg)
\end{align}$$
4.5、PPO
近端策略优化(Proximal Policy Optimization)
- 目标函数
$$\begin{align}
\mathcal{L}_{\textit{PPO}}(\bm{\theta})
&=\mathbb{E}_{q\sim \rho(Q),\bm{o}\sim \pi_{\bm{\theta}_\text{old}}}\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}\bigg[\min\left[\frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\text{old}}(o_t\mid q,o_{:t})},\mathrm{\text{clip}}\left[\frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\text{old}}(o_t\mid q,o_{:t})},1-\epsilon,1+\epsilon\right]\right]\cdot A_{\pi}(q,o_t)\bigg]
\end{align}$$
为了简化分析,假定模型在每个探索阶段之后只有一个更新,从而确保 $\pi_{\textit{old}}=\pi_{\bm{\theta}}$,在这种情况下,删除最小值和裁剪操作有简化的目标函数
$$\begin{align}
\mathcal{L}_{\textit{PPO}}(\bm{\theta})
&=\mathbb{E}_{q\sim \rho(Q),\bm{o}\sim \pi_{\bm{\theta}_\text{old}}}\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}\bigg[
\frac{\pi_{\bm{\theta}}(o_t\mid q,o_{:t})}{\pi_{\bm{\theta}_\text{old}}(o_t\mid q,o_{:t})}\cdot A_{\pi}(q,o_t)
\bigg]
\end{align}$$
- 数据集
PPO是问题 $q$上的探索数据轨迹(输出结果),$\bm{o}=[o_1,\cdots,o_{|\bm{o}|}]$是回答的每个token。
$$\begin{align}
\mathcal{D}=\{(q_i,\bm{o}_i)\}_{i=1}^n
\end{align}$$
梯度系数
$$\begin{align}
\nabla_{\bm{\theta}}\mathcal{L}_{\textit{PPO}}(\bm{\theta})
&=\mathbb{E}_{q\sim \rho(Q),\bm{o}\sim \pi_{\bm{\theta}_\text{old}}}\frac{1}{|\bm{o}|}\sum_{t=1}^{|\bm{o}|}\bigg[
\nabla_{\bm{\theta}}\log\pi_{\bm{\theta}}(o_t\mid q,o_{:t})\cdot A_{\pi}(q,o_t)
\bigg]
\end{align}$$奖励函数
奖励函数就是已经训练好的奖励模型
$$\begin{align}
\pi_{\bm{\theta}_\textit{rm}}
\end{align}$$梯度系数
$$\begin{align}
\textit{GC}_{\textit{PPO}}(q,o,r,\pi_{\bm{\theta}_\textit{rm}},v_{\bm{w}})=A_t(q,o_t)
\end{align}$$
4.6、GRPO
组相对策略优化(Group Relative Policy Optimization)
- 目标函数
和PPO一样简化,删除最小值和裁剪操作,有简化的目标函数:
$$\begin{align}
\mathcal{L}_{\textit{GRPO}}(\bm{\theta})
=\mathbb{E}_{q\sim \rho(Q),\{\bm{o}_i\}_{i=1}^G\sim \pi_{\bm{\theta}_\text{old}}}\frac{1}{G}\sum_{i=1}^G
\bigg[\frac{\pi_{\bm{\theta}}(\bm{o}_{i}\mid q)}{\pi_{\bm{\theta}_\text{old}}(\bm{o}_{i}\mid q)}
\cdot A_{\pi}(q,\bm{o}_i)-\beta\left(\frac{\pi_{\bm{\theta}_\textit{ref}}(\bm{o}_{i}\mid q)}{\pi_{\bm{\theta}}(\bm{o}_{i}\mid q)}- \log \frac{\pi_{\bm{\theta}_\textit{ref}}(\bm{o}_{i}\mid q)}{\pi_{\bm{\theta}}(\bm{o}_{i}\mid q)}-1\right)\bigg]
\end{align}$$
- 数据集
GRPO是在一个问题 $q$上的探索一组数据轨迹(输出结果),$\bm{o}=[o_1,\cdots,o_{|\bm{o}|}]$是回答的每个token。
$$\begin{align}
\mathcal{D}=\{(q_i,\{\bm{o}_{i,g}\}_{g=1}^G)\}_{i=1}^n
\end{align}$$
- 梯度系数
$$\begin{align}
\nabla_{\bm{\theta}}\mathcal{L}_{\textit{GRPO}}(\bm{\theta})
=\mathbb{E}_{q\sim \rho(Q),\{\bm{o}_i\}_{i=1}^G\sim \pi_{\bm{\theta}_\text{old}}}\frac{1}{G}\sum_{i=1}^G
\left[
\bigg[
A_{\pi}(q,\bm{o}_i)
+\beta\left(\frac{\pi_{\bm{\theta}_\textit{ref}}(\bm{o}_{i}\mid q)}{\pi_{\bm{\theta}}(\bm{o}_{i}\mid q)}-1\right)
\bigg]
\nabla_{\bm{\theta}}\log \pi_{\bm{\theta}}(\bm{o}_{i}\mid q)
\right]
\end{align}$$
奖励函数
奖励的计算基于规则、代码验证器、格式验证来计算的梯度系数
$$\begin{align}
\textit{GC}_{\textit{GRPO}}(q,o,r,\pi_{\bm{\theta}_\textit{rm}})
=A_{\pi}(q,\bm{o}_i)
+\beta\left(\frac{\pi_{\bm{\theta}_\textit{ref}}(\bm{o}_{i}\mid q)}{\pi_{\bm{\theta}}(\bm{o}_{i}\mid q)}-1\right)
\end{align}$$
参考文献
[^1]: DeepSeek-AI, Guo, D., Yang, D., Zhang, H., Song, J., Zhang, R., et al. (2025, January 22). DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning. arXiv. https://doi.org/10.48550/arXiv.2501.12948
[^2]: Schulman, J., Moritz, P., Levine, S., Jordan, M., & Abbeel, P. (2018, October 20). High-Dimensional Continuous Control Using Generalized Advantage Estimation. arXiv. https://doi.org/10.48550/arXiv.1506.02438
[^3]: Schulman, J., Wolski, F., Dhariwal, P., Radford, A., & Klimov, O. (2017, August 28). Proximal Policy Optimization Algorithms. arXiv. https://doi.org/10.48550/arXiv.1707.06347
[^4]: Shao, Z., Wang, P., Zhu, Q., Xu, R., Song, J., Bi, X., et al. (2024, April 27). DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models. arXiv. https://doi.org/10.48550/arXiv.2402.03300
[^5]: J. Schulman. Approximating kl divergence, 2020. URL http://joschu.net/blog/kl-approx.html.
| 版权声明 |  |
| 由引线小白创作并维护的柠檬CC博客采用署名-非商业-禁止演绎4.0国际许可证。 本文首发于柠檬CC [ https://www.limoncc.com ] , 版权所有、侵权必究。 | |
| 本文永久链接 | httpss://www.limoncc.com/post/c0a3be9c86b2b4cd/ |
| 如果您需要引用本文,请参考: |
| 引线小白. (Jan. 31, 2025). 《大模型中的强化学习——大语言模型研究05》[Blog post]. Retrieved from https://www.limoncc.com/post/c0a3be9c86b2b4cd |
| @online{limoncc-c0a3be9c86b2b4cd, title={大模型中的强化学习——大语言模型研究05}, author={引线小白}, year={2025}, month={Jan}, date={31}, url={\url{https://www.limoncc.com/post/c0a3be9c86b2b4cd}}, } |