作者: 引线小白-本文永久链接:httpss://www.limoncc.com/post/c7d551950374c4114400ca0e635169ba/
知识共享许可协议: 本博客采用署名-非商业-禁止演绎4.0国际许可证
摘要:本文意在理清广义线性模型的问题。若有错误,请大家指正。
关键词:广义线性模型,广义线性混合模型,指数族,probit 回归
一、 简述
我们现在遇到了各种各样的概率分布:高斯分布、伯努利分布、学生 $\displaystyle \text{t}$分布、均匀分布、伽玛分布等等,这些都是广义分布的广义函数,称为指数族。在本章中,我们将讨论这个家族的各种性质。这使我们能够得到具有非常广泛适用性的定理和算法。
我们将会看到,如何方便地将指数家族中的任何成员作为一个类条件密度,以便做一个生成分类器。此外,我们还将讨论如何建立判别模型,其中的响应变量有指数族分布,其均值是输入的线性函数;这被称为广义线性模型,并将 $\displaystyle \textit{logistic } $回归中的概念推广到其他类型的响应变量中。
二、 指数族
在定义指数族之前,我们先提几个重要原因:
•可以证明,在一定的规律性条件下,指数族是唯一具有有限大小统计量的分布族,这意味着我们可以将数据压缩成一个固定大小的摘要,而不会丢失信息。这对于在线学习特别有用,我们稍后会看到。
•指数族是有共轭先验分布存在的唯一分布族,这简化了后验计算。
•在满足一些约束的假设下,指数族是熵最大的一个分布家族。
•指数族是广义线性模型的核心。
•指数族是变分推断的核心。
2.1、定义
参数为 $\displaystyle \bm{w} $,变量为 $\displaystyle \bm{x} $ 的指数分布族定义为下面形式的概率分布集合:
$$
\begin{align}
p(\bm{x}\mid \bm{w})
&=\frac{1}{Z(\bm{w})}h(\bm{x})\exp\left[\bm{w}^\text{T}\bm{T}(\bm{x})\right]
=h(\bm{x})\exp\big[\bm{w}^\text{T}\bm{T}(\bm{x})-A(\bm{w})\big]\
\end{align}
$$
特别的为了适合上述形式,参数通常是需要变形 $\displaystyle \bm{\eta}=\bm{\eta}(\bm{w})$,于是有:
$$\begin{align}
p(\bm{x}\mid \bm{w})
&=\frac{1}{Z(\bm{w})}h(\bm{x})\exp\left[\bm{\eta}(\bm{w})^\text{T}\bm{T}(\bm{x})\right]\\\\
&=h(\bm{x})\exp\left[\bm{\eta}(\bm{w})^\text{T}\bm{T}(\bm{x})-A(\bm{\eta}(\bm{w}))\right]\\\\
&=\exp\left[\bm{\eta}(\bm{w})^\text{T}\bm{T}(\bm{x})-A\left(\bm{\eta}(\bm{w})\right)+B(\bm{x})\right]\\\\
&=h(\bm{x})g(\bm{\eta})\exp\left[\bm{\eta}(\bm{w})\cdot\bm{T}(\bm{x})\right]
\end{align}$$其中:
$\displaystyle Z(\bm{w})=\int_{\mathcal{X}^n}h(\bm{x})\exp\left[\bm{\eta^\text{T}(\bm{w})}\bm{T}(\bm{x})\right]\mathrm{d}\bm{x}$
$\displaystyle A(\bm{w})=\ln Z(\bm{w}) $
1、$\displaystyle \bm{w} $叫做自然参数 $\displaystyle \textit{(natural parameters)} $、$\displaystyle \bm{\eta(\bm{w})} $叫做规范参数 $\displaystyle \textit{(canonical parameters)} $ 。如果 $\displaystyle \dim(\bm{w})<\dim(\bm{\eta}) $,称分布为曲线指数族 $\displaystyle \textit{(curved exponential family)} $。这意味比参数更多的充分统计量。
2、 $\displaystyle \bm{T}(\bm{x})\in\mathbb{R}^k $叫做充分统计向量 $\displaystyle \textit{(vector of sufficient statistics)} $。
3、$\displaystyle Z(\bm{w}) $叫做配分函数 $\displaystyle \textit{(partition function)} $
4、$\displaystyle A(\bm{w}) $叫做对数配分函数 $\displaystyle \textit{(log partition function)} $或者累积量函数 $\displaystyle \textit{(cumulant function)} $
5、$\displaystyle h(\bm{x}) $叫做放缩常量 $\displaystyle \textit{(scaling constant)} $,通常是1。
6、特别的 $\displaystyle \bm{T}(\bm{x})=\bm{x} $ 称为自然指数族 $\displaystyle \textit{(natural exponential family)} $或者规范形 $\displaystyle \textit{(canonical form)} $
2.2、对数配分函数
指数族的一个重要性质是对数配分函数的导数可以用来生成充分统计量的累积量。所以 $\displaystyle A \big(\bm{\eta}\big)$有时被称为累积量函数。
$$\begin{align}
A(\bm{\eta})=\ln \bigg[\int h(\bm{x})\exp \big[\bm{\eta}^\text{T}\bm{T}(\bm{x})\big]d \bm{x}\bigg]
\end{align}$$
于是有
$$\begin{align}
\dot{A}(\bm{\eta})=\frac{\partial A}{\partial \bm{\eta}}
&=\frac{\displaystyle\frac{\partial }{\partial \bm{\eta}}\bigg[\int h(\bm{x})\exp \big[\bm{\eta}^\text{T}\bm{T}(\bm{x})\big]d \bm{x}\bigg]}{\displaystyle\int h(\bm{x})\exp \big[\bm{\eta}^\text{T}\bm{T}(\bm{x})\big]d \bm{x}}
=\frac{\displaystyle \int h(\bm{x})\exp \big[\bm{\eta}^\text{T}\bm{T}(\bm{x})\big]\bm{T}d \bm{x}}{\exp \big[A(\bm{\eta})\big]}\\\\
&=\int \bm{T} \cdot h(\bm{x})\exp \big[\bm{\eta}^\text{T}\bm{T}(\bm{x})-A(\bm{\eta})\big]d \bm{x}\\\\
&=\int \bm{T} \cdot p \big(\bm{x}\big)d \bm{x}
=\mathrm{E}\big[\bm{T}(\bm{x})\big]
\end{align}$$
还有:
$$\begin{align}
\ddot{A}(\bm{\eta})=\frac{\partial^2 A}{\partial \bm{\eta}\partial\bm{\eta}^\text{T}}
&=\frac{\partial }{\partial \bm{\eta}^\text{T}}\bigg[\int \bm{T} \cdot h(\bm{x})\exp \big[\bm{\eta}^\text{T}\cdot\bm{T}-A(\bm{\eta})\big]d \bm{x}\bigg]\\\\
&=\int \bm{T}^\text{T}\cdot h(\bm{x})\exp \big[\bm{\eta}^\text{T}\cdot\bm{T}-A(\bm{\eta})\big]\big[\bm{T}-\dot{A}(\bm{\eta})\big]d \bm{x}\\\\
&=\int \bm{T}^\text{T}\big[\bm{T}-\dot{A}(\bm{\eta})\big]p (\bm{x})d \bm{x}\\\\
&=\mathrm{E}\big[\bm{T}^\text{T}\bm{T}\big]- \mathrm{E}\big[\bm{T}^\text{T}\big]\mathrm{E}\big[\mathrm{E}\big[\bm{T}\big]\big]
=\mathrm{E}\big[\bm{T}^\text{T}\bm{T}\big]-\mathrm{E}^\text{T}\big[\bm{T}\big]\mathrm{E}\big[\bm{T}\big]\\\\
&=\mathrm{cov}\big[\bm{T}(\bm{x})\big]
\end{align}$$
也就是说
$$\begin{align}
\nabla^2A \big(\bm{\eta}\big)=\mathrm{cov}\big[\bm{T}(\bm{x})\big]
\end{align}$$
由于协方差是正定的,我们看到一个 $\displaystyle A \big(\bm{\eta}\big)$是一个凸函数(参见7.3.3)。注意上面的推导交换了积分和求导顺序,这需要满足一致收敛条件。这显然是满足的。
2.3、例子
让我们考虑一些例子来让事情更清楚些。
2.3.1、 $\displaystyle \textit{0-1}$分布
有 $\displaystyle x\in\{0,1\}$的 $\displaystyle \textit{0-1}$分布写成指数族形式:
$$\begin{align}
\mathrm{Ber}\big(x\mid \mu\big)=\mu^x(1-\mu)^{1-x}=\exp \big[x\ln \mu+(1-x)\ln (1-\mu)\big]=\exp \big[\bm{\eta}^\text{T}\bm{T}(x)\big]
\end{align}$$
其中:
$\displaystyle \bm{\eta}=\big[\ln \mu,\ln (1-\mu)\big]^\text{T}$
$\displaystyle \bm{T}(x) =\big[\mathbb{I}\big(x=0\big),\mathbb{I}\big(x=1\big)\big]^\text{T}
$
然后这个表示是过于完备以至于很啰嗦,因为特征之间有线性关系,这很不简洁。
$$\begin{align}
\bm{I}^\text{T}\bm{T}(x)=\mathbb{I}\big(x=0\big)+\mathbb{I}\big(x=1\big)=1
\end{align}$$
因为 $\displaystyle \bm{\eta}$不是唯一的,这要求我们 $\displaystyle \bm{\eta}$最好是最简洁的。也就是说分布均值和唯一的 $\displaystyle \bm{\eta}$联系。这样我们可以定义:
$$\begin{align}
\mathrm{Ber}\big(x\mid \mu\big)=(1-\mu)\exp \bigg[x\ln \bigg(\frac{\mu}{1-\mu}\bigg)\bigg]
\end{align}$$
现在 $\displaystyle \eta=\ln \bigg(\frac{\mu}{1-\mu}\bigg)$这是 $\displaystyle \textit{log-odds ratio} $,$\displaystyle T(x)=x$, $\displaystyle Z=1/(1-\mu)$。于是有:
$$\begin{align}
A(\eta)=\ln Z=\ln \bigg(\frac{1}{1-\mu}\bigg)=\ln \big[1+\mathrm{e}^\eta\big]
\end{align}$$
来自规范参数的均值 $\displaystyle \mu$
$$\begin{align}
\mu=\dot{A}(\eta)=\mathrm{sigm}\big(\eta\big)=\frac{1}{1+\mathrm{e}^{-\eta}}=\eta^{-1}(\mu)
\end{align}$$
2.3.2 、分类分布
令 $\displaystyle x_i=\mathbb{I}(x=i)$,分类分布指数族形式是:
$$\begin{align}
\mathrm{Cat}\big(\bm{x}\mid \bm{\mu}\big)
&=\prod_{i=1}^c\mu_i^{x_i}=\exp \Bigg[\sum_{i=1}^cx_i\ln \mu_i\Bigg]\\\\
&=\exp \Bigg[\sum_{i=1}^{c-1}x_i\ln \mu_i+\bigg(1-\sum_{j=1}^{c-1}x_j\bigg)\ln \bigg(1-\sum_{j=1}^{c-1}\mu_j\bigg)\Bigg]\\\\
&=\exp \Bigg[\sum_{i=1}^{c-1}x_i\ln \bigg(\frac{\mu_i}{1-\sum_{j=1}^{c-1}\mu_j}\bigg)+\ln\bigg(1-\sum_{j=1}^{c-1}\mu_j\bigg)\Bigg]\\\\
&=\exp\Bigg[\sum_{i=1}^{c-1}x_i\ln \bigg(\frac{\mu_i}{\mu_c}\bigg)+\ln \mu_c\Bigg]
\end{align}$$ 其中 $\displaystyle \mu_c=1-\sum_{j=1}^{c-1}\mu_j$,有:
$$\begin{align}
\mathrm{Cat}\big(\bm{x}\mid \bm{\mu}\big)
&=\exp \big[\bm{\eta}^\text{T}\bm{T}\big(\bm{x}\big)-A \big(\bm{w}\big)\big]
\end{align}$$
其中
$\displaystyle \bm{\eta}=\big[\ln \frac{\mu_1}{\mu_c},\cdots,\ln \frac{\mu_{c-1}}{\mu_c}\big]^\text{T}$
$\displaystyle \bm{T}\big(\bm{x}\big)=\bm{x}=\big[\mathbb{I}(x=1),\cdots,\mathbb{I}(x=c-1)\big]^\text{T}$
同样,我们可以通过使用的规范参数来恢复均值参数
$$\begin{align}
\mu_i=\frac{\mathrm{e}^{\eta_i}}{1+\sum_{j=1}^{c-1}\mathrm{e}^{\eta_j}}
\end{align}$$易知:$$\begin{align}
\mu_c
=1-\frac{\sum_{i=1}^{c-1}\mathrm{e}^{\eta_i}}{1+\sum_{j=1}^{c-1}\mathrm{e}^{\eta_j}}
=\frac{1}{1+\sum_{j=1}^{c-1}\mathrm{e}^{\eta_j}}
\end{align}$$亦有$$\begin{align}
A \big(\bm{\eta}\big)=\ln \bigg(1+\sum_{i=1}^{c-1}\mathrm{e}^{\eta_i}\bigg)
\end{align}$$如果我们定义 $\displaystyle \eta_c=0\to \mu_{i=c}=0$,那么有 $\displaystyle \bm{\eta}:=\big[\bm{\eta}^\text{T},0\big]^\text{T}$, $\displaystyle \bm{T}:=\big[\bm{T}^\text{T},\mathbb{I}\big(x=c\big)\big]^\text{T}$
$$\begin{align}
\mathrm{Cat}\big(\bm{x}\mid \bm{\mu}\big)
&=\exp \big[\bm{\bm{\eta}^\text{T}T}\big(\bm{x}\big)-A \big(\bm{\eta}\big)\big]
\end{align}$$其中 $\displaystyle A \big(\bm{\eta}\big)=\ln \bigg(\sum_{i=1}^{c}\mathrm{e}^{\eta_i}\bigg)\\\\$,特别的有:$$\begin{align}
\bm{\mu}&=\mathcal{S}\big(\bm{\eta}\big)=\bm{\eta}^{-1}\big(\bm{\mu}\big)
\end{align}$$
这样我们就通过指数族建立了 $\displaystyle \textit{sigm}$ 函数与 $\displaystyle \textit{0-1} $分布、 $\displaystyle \textit{softmax} $函数与分类分布的联系。换句话说 $\displaystyle \textit{sigm} $ 函数、 $\displaystyle \textit{softmax} $ 函数是连接函数的逆函数。这也是sigm和sofmax函数在机器学习,人工智能广泛应用的原因,因为只要分类问题,就必然涉及。
2.3.3、单变量高斯
单变量高斯可以写成指数族形式,如下:
$$\begin{align}
\mathcal{N}\big(x\mid \mu,\sigma^2\big)
&=\big(2\pi\sigma^2\big)^{-1/2}\exp \big[\frac{1}{2\sigma^2}\big(x-\mu\big)^2\big]\\\\
&=\big(2\pi\sigma^2\big)^{-1/2}\exp \big[\frac{\mu^2}{2\sigma^2}\big]\exp \big[-\frac{1}{2\sigma^2}x^2+\frac{\mu}{\sigma^2}x\big]\\\\
&=\frac{1}{Z \big(\bm{\eta}\big)}\exp \big[\bm{\eta}^\text{T}\bm{T}(x)\big]
\end{align}$$
其中:
$\displaystyle \bm{\eta}=\big[\frac{\mu}{\sigma^2},-\frac{1}{2\sigma^2}\big]^\text{T}$
$\displaystyle \bm{T}(x)=\big[x,x^2\big]^\text{T}$
$\displaystyle Z \big(\bm{\eta}\big)=\big(2\pi\sigma^2\big)^{-1/2}\exp \big[\frac{\mu^2}{2\sigma^2}\big] $
$\displaystyle A \big(\bm{\eta}\big)=\ln Z \big(\bm{\eta}\big)=-\frac{\eta_1^2}{4\eta_2}-\frac{1}{2}\ln \big(-2\eta_2\big)-\frac{1}{2}\ln 2\pi$
2.2.4、非例子
并非所有的分布都属于指数族。例如均匀分布 $\displaystyle x\sim \mathrm{U}[a,b]$ 就不是,因为分布支撑集 $\displaystyle \mathcal{X}$取决于参数。此外学生 $\displaystyle T$分布也不属于,因为它没有必要的形式。$\displaystyle \textit{Pitman - Koopman - Darmois} $定理指出,在一定规范条件下,指数家族是唯一具有有限统计量的分布族。(在这里,大小有限与数据集的大小无关。)这个定理要求的条件之一是,分布支撑集 $\displaystyle \mathcal{X}$不依赖于参数。对于这样分布的简单示例:均匀分布
$$\begin{align}
p(x\mid w)=\mathrm{U}(x\mid w)=\frac{\mathbb{I}\big(0\leqslant x\leqslant w\big)}{w}
\end{align}$$
似然函数是:
$$\begin{align}
p \big(\mathcal{D}\big)=w^{-n}\mathbb{I}\big(0\leqslant\max\{x_i\}\leqslant w\big)
\end{align}$$
因此充分统计量是 $\displaystyle n$和 $\displaystyle T=\max_{i}x_i$。它是有限的,但均匀分布并不在指数家族中。因为它的支撑集 $\displaystyle \mathcal{X}=[0,w]$ 依赖于参数 $\displaystyle w$。
2.4、指数族的 $\displaystyle \textit{MLE}$
指数家族模型似然函数:
$$\begin{align}
p \big(\mathcal{D}\mid \bm{w}\big)
&=\frac{1}{Z^n(\bm{w})}\bigg[\prod_{i=1}^n h(\bm{x}_i)\bigg]\exp \bigg[\bm{\eta}^\text{T}(\bm{w})\sum_{i=1}^n \bm{T}(\bm{x}_i)\bigg]\\\\
&=\bigg[\prod_{i=1}^n h(\bm{x}_i)\bigg]\exp \bigg[\bm{\eta}^\text{T}(\bm{w})\bm{T}(\mathcal{D})-nA \big(\bm{\eta}\big)\bigg]
\end{align}$$
易见似然函数也是指数族,它的充分统计量是 $\displaystyle n$和
$$\begin{align}
\bm{T}\big(\mathcal{D}\big)=\bigg[\sum_{i=1}^n T_1(\bm{x}_i),\cdots,\sum_{i=1}^nT_k(\bm{x}_i)\bigg]^\text{T}
\end{align}$$
例如伯努利分布我们有 $\displaystyle \bm{T}=\bigg[\sum_{i=1}^n \mathbb{I}(\bm{x}_i)\bigg]$和单变量高斯分布 $\displaystyle \bm{T}=\big[\sum_{i=1}^nx_i,\sum_{i=1}^nx_i^2\big]$(我们也需要知道样本大小 $\displaystyle n$)
现在我们给定 $\displaystyle \mathrm{idd}$数据集 $\displaystyle \mathcal{D}=\{\bm{x}_i\}_{i=1}^n$,用标准指数家族模型来计算 $\displaystyle \textit{MLE} $。对数似然函数:
$$\begin{align}
\ell(\bm{\eta})=\ln p \big(\mathcal{D}\mid \bm{\eta}\big)
=\bigg[\sum_{i=1}^n\ln h(\bm{x}_i)\bigg]+\bigg[\bm{\eta}^\text{T}(\bm{w})\bm{T}(\mathcal{D})-nA \big(\bm{\eta}\big)\bigg]
\end{align}$$
因为 $\displaystyle -A \big(\bm{\eta}\big)$关于 $\displaystyle \bm{\eta}$是凹的, $\displaystyle \bm{\eta}^\text{T}(\bm{w})\bm{T}(\mathcal{D})$关于 $\displaystyle \bm{\eta}$是线性的。故对数似然是凹的,因此有唯一的全局最大值。为了得到这个最大值,利用关于对数分配函数导数是充分统计量期望的结论有:
$$\begin{align}
\frac{\partial \ell}{\partial \bm{\eta}}=\bm{T}(\mathcal{D})-n \mathrm{E}\big[\bm{T}(\bm{x})\big]=\bm{0}
\end{align}$$有:$$\begin{align}
\mathrm{E}\big[\bm{T}(\bm{x})\big]=\frac{1}{n}\bm{T}\big(\mathcal{D}\big)
\end{align}$$
充分统计量的经验平均值必须等于模型充分统计量的理论期望,即 $\displaystyle \hat{\bm{\eta}}$必须满足上式。这叫做矩匹配 $\displaystyle \textit{(moment matching)} $。例如在伯努利分布中,我们有 $\displaystyle T(\mathcal{D})=\sum_{i=1}^n \mathbb{I}\big(x_i=1\big)$有:
$$\begin{align}
\mathrm{E}\big[\bm{T}(\bm{x})\big]=\hat{\mu}=\frac{1}{n}\sum_{i=1}^n \mathbb{I}\big(x_i=1\big)
\end{align}$$
2.5、指数族的贝叶斯
我们已经看到,如果先验概率是共轭的,那么精确贝叶斯分析是相当简单的。非正式这意味着先验 $\displaystyle p \big(\bm{\eta}\mid \bm{\tau}\big)$与似然函数 $\displaystyle p \big(\mathcal{D}\mid \bm{\eta}\big)$有相同形式。为了这个有意义,我们要求似然函数的充分统计量是有限,所以我们可以写 $\displaystyle p \big(\mathcal{D}\mid \bm{\eta}\big)=p \big(\bm{T}(\mathcal{D})\mid \bm{\eta}\big)$。这表明,唯一有共轭先验的分布族是指数族。稍后我们将推导先验和后验。
2.5.1、似然函数
我们多角度地写出指数族似然函数:
$$\begin{align}
p \big(\mathcal{D}\mid \bm{w}\big)
&=\frac{1}{Z^n(\bm{w})}\bigg[\prod_{i=1}^n h(\bm{x}_i)\bigg]\exp \bigg[\bm{\eta}^\text{T}(\bm{w})\bm{T}(\mathcal{D})\bigg]\\\\
&\propto\exp \bigg[\bm{\eta}^\text{T}(\bm{w})\bm{T}(\mathcal{D})-nA \big(\bm{\eta}\big)\bigg]\\\\
&\propto\exp \bigg[n\bm{\eta}^\text{T}\bar{\bm{T}}-nA \big(\bm{\eta}\big)\bigg]
\end{align}$$
其中 $\displaystyle \bar{\bm{T}}=\frac{1}{n}\bm{T}(\mathcal{D})$
2.5.2、先验
共轭先验有如下形式:
$$\begin{align}
p \big(\bm{\eta}\mid \kappa_0,\bm{\tau}_0\big)
\propto g^{\kappa_0}(\bm{\eta})\exp \big[\bm{\eta}^\text{T}(\bm{w})\bm{\tau}_0\big]
\end{align}$$
令 $\displaystyle \bm{\tau}=\kappa_0\bar{\bm{\tau}}_0$,这样我们分离出先验的虚数据集大小 $\displaystyle \kappa_0$,和虚数据集充分统计量均值 $\displaystyle \bar{\bm{\tau}}_0$。在规范形式中,先验成为:
$$\begin{align}
p \big(\bm{\eta}\mid \kappa_0,\bar{\bm{\tau}}_0\big)
\propto \exp \big[\kappa_0\bm{\eta}^\text{T}\bar{\bm{\tau}}_0-\kappa_0A(\bm{\eta})\big]
\end{align}$$
2.5.3、后验
有后验
$$\begin{align}
p \big(\bm{\eta}\mid \mathcal{D}\big)
= p \big(\bm{\eta}\mid \kappa_n,\bm{\tau}_n\big)
=p \big(\bm{\eta}\mid \kappa_0+n,\bm{\tau}_0+\bm{T}\big)
\end{align}$$
上式更新了超参。在规范形式下变成了
$$\begin{align}
p \big(\bm{\eta}\mid \mathcal{D}\big)
= p \big(\bm{\eta}\mid \kappa_n,\bar{\bm{\tau}}_n\big)
=p \big(\bm{\eta}\mid \kappa_0+n,\frac{ \kappa_0\bar{\bm{\tau}}_0+n\bar{\bm{T}}}{\kappa_0+n}\big)
\end{align}$$
因此我们看到后验超参是先验超参均值和充分统计量平均值一个凸组合。
2.5.4、后验预测密度
下面我们鉴于过去的数据集 $\displaystyle \mathcal{D}_t$,推导未来观测 $\displaystyle \mathcal{D}_{t+1}$的一个通用的预测密度的表达式。为简洁记,我们将把充分统计量与数据集大小写在一起: $\displaystyle \tilde{\bm{\tau}}_0=[\kappa_0;\bm{\tau}_0]$、 $\displaystyle \tilde{\bm{T}}_t=\big[n;\bm{T}\big(\mathcal{D}_t\big)\big]$、 $\displaystyle \tilde{\bm{T}}_{t+1}=\big[n;\bm{T}\big(\mathcal{D}_{t+1}\big)\big]$。先验、后验有:
$$\begin{align}
p \big(\bm{\eta}\mid \tilde{\bm{\tau}}_0\big)
=\frac{1}{Z( \tilde{\bm{\tau}}_0)}g^{\kappa_0}(\bm{\eta})\exp \big[\bm{\eta}^\text{T}(\bm{w})\bm{\tau}_0\big]
\end{align}$$
$$\begin{align}
p \big(\bm{\eta}\mid \mathcal{D}_t\big)
&= \frac{p \big(\bm{\eta}\mid \tilde{\bm{\tau}}_0\big)p \big(\mathcal{D}_t\mid \bm{\eta}\big)}{p(\mathcal{D}_t)}
=p \big(\bm{\eta}\mid \tilde{\bm{\tau}}_0+\tilde{\bm{T}}_t\big)\\\\
&=\frac{1}{Z( \tilde{\bm{\tau}}_0+\tilde{\bm{T}}_t)}g^{\kappa_0+n_t}(\bm{\eta})\exp \big[\bm{\eta}^\text{T}(\bm{w})\big[\bm{\tau}_0+\bm{T}_t\big]\big]
\end{align}$$
$\displaystyle p \big(\mathcal{D}_{t+1}\mid \bm{\eta}\big)=\bigg[\prod_{i=1}^{n_{t+1}} h(\bm{x}_i)\bigg]g^{n_{t+1}}\big(\bm{\eta}\big)\exp \big[\bm{\eta}^\text{T}(\bm{w})\bm{T}_{t+1}\big]$那么后验预测为:$$\begin{align}
p \big(\mathcal{D}_{t+1}\mid \mathcal{D}_t\big)
&=\int p \big(\mathcal{D}_{t+1}\mid \bm{\eta}\big)p \big(\bm{\eta}\mid \mathcal{D}_t\big)d \bm{\eta}\\\\
&=\int\bigg[\prod_{i=1}^{n_{t+1}} h(\bm{x}_i)\bigg]g^{n_{t+1}}\big(\bm{\eta}\big)\exp \big[\bm{\eta}^\text{T}(\bm{w})\bm{T}_{t+1}\big]\frac{1}{Z( \tilde{\bm{\tau}}_0+\tilde{\bm{T}}_t)}g^{\kappa_0+n_t}(\bm{w})\exp \big[\bm{\eta}^\text{T}(\bm{w})\big[\bm{\tau}_0+\bm{T}_t\big]\big]d \bm{\eta}\\\\
&=\bigg[\prod_{i=1}^{n_{t+1}} h(\bm{x}_i)\bigg] \frac{1}{Z( \tilde{\bm{\tau}}_0+\tilde{\bm{T}}_t)}\int g^{\kappa_0+n_t+n_{t+1}}\big(\bm{w}\big)\exp \big[\bm{\eta}^\text{T}(\bm{w})\big[\bm{\tau}_0+\bm{T}_t+\bm{T}_{t+1}\big]\big]d \bm{\eta}\\\\
&=\bigg[\prod_{i=1}^{n_{t+1}} h(\bm{x}_i)\bigg] \frac{Z\big( \tilde{\bm{\tau}}_0+\tilde{\bm{T}}_t+\tilde{\bm{T}}_{t+1}\big)}{Z\big( \tilde{\bm{\tau}}_0+\tilde{\bm{T}}_t\big)}
\end{align}$$
的可能性和后部有一个类似的形式。因此如果 $\displaystyle n_t = 0$,这就变成了 $\displaystyle \mathcal{D}_{t+1}$的边际分布,这是我们熟悉后验的归一乘以一个常数。
2.5.5、伯努利分布举例
作为一个简单的例子,我们用新表示法来重新讨论一下:贝塔-伯努利模型。
似然函数是
$$\begin{align}
p \big(\mathcal{D}\mid \mu\big)=(1-\mu)^n\exp \bigg[\ln \bigg(\frac{\mu}{1-\mu}\bigg)\sum_{i=1}^n x_i\bigg]
\end{align}$$
共轭先验是:
$$\begin{align}
p \big(\mu\mid \kappa_0,\tau_0\big)
&\propto (1-\mu)^{\kappa_0}\exp \bigg[\ln \bigg(\frac{\mu}{1-\mu}\bigg)\tau_0\bigg]=\mu^{\tau_0}\big(1-\mu\big)^{\kappa_0-\tau_0}
\end{align}$$
如果我们定义 $\displaystyle a_0=\tau_0+1$和 $\displaystyle b_0=\kappa_0-\tau_0+1$,我们可以看到这是一个贝塔分布。
我们可以推导出后验,其中 $\displaystyle T=\sum_{i=1}^n \mathbb{I}\big(x_i=1\big)$是充分统计量:
$$\begin{align}
p \big(\mu\mid \mathcal{D}\big)
&\propto \mu^{\tau_0+T}\big(1-\mu\big)^{\kappa_0-\tau_0+n-T}\\\\
&=\mu^{\tau_n}\big(1-\mu\big)^{\kappa_n-\tau_n}\\\\
&=\mu^{a_n-1}\big(1-\mu\big)^{b_n-1}
\end{align}$$其中 $\displaystyle a_n=\tau_n+1$、 $\displaystyle b_n=\kappa_n-\tau_n+1$
我们可以推导出后验的预测分布。假设 $\displaystyle p (\mu)=\mathrm{Beta}\big(\mu\mid a_0,b_0\big)$,并让 $\displaystyle T_t=T(\mathcal{D}_t)$是硬币正面在过去的数量。我们可以预测给定一个未来序列 $\displaystyle \mathcal{D}_{t+1}$的出现正面的概率。令这个序列的充分统计量 $\displaystyle T_{t+1}=\sum_{i=1}^m \mathbb{I}\big(x_i^{t+1}=1\big)$
$$\begin{align}
p \big(\mathcal{D}_{t+1}\mid \mathcal{D}_t\big)
&=\int_0^1 p \big(\mathcal{D}_{t+1}\mid \mu\big)p \big(\mu\mid \mathcal{D}_t\big)d\mu\\\\
&=\int_0^1 p \big(\mathcal{D}_{t+1}\mid \mu\big)\mathrm{Beta} \big(\mu\mid a_{t},b_{t}\big)d\mu\\\\
&=\frac{\Gamma(a_t+b_t)}{\Gamma{a_t}\Gamma(b_t)}\int_0^1 \mu^{a_t+T_{t+1}-1}\big(1-\mu\big)^{b_t+m-T_{t+1}-1}\\\\
&=\frac{\Gamma(a_t+b_t)}{\Gamma{a_t}\Gamma(b_t)}\int_0^1 \mu^{a_{t+1}-1}\big(1-\mu\big)^{b_{t+1}-1}\\\\
&=\frac{\Gamma(a_t+b_t)}{\Gamma(a_t)\Gamma(b_t)}
\frac{\Gamma(a_{t+1})\Gamma(b_{t+1})}{\Gamma(a_{t+1}+b_{t+1})}
\end{align}$$
其中
$\displaystyle a_{t+1}=a_t+T_{t+1}=\tau_0+T_t+1+T_{t+1}$
$\displaystyle b_{t+1}=\kappa_n-\tau_n+1=\kappa_0+n-(\tau_0+T_t)+1+m-T_{t+1}$
2.6、指数族与最大熵原理 $\displaystyle \textit{(Maximum Entropy)} $
虽然指数家族很方便,但对它的使用有更深层次的理由吗?事实存在这样的情况:如果用最少约束来假设数据,特别是假设某些特征或函数的期望
$$\begin{align}
\int \bm{\phi}(\bm{x})p(\bm{x})d \bm{x}=\mathrm{E}\big[\bm{\phi}\big]=\bm{\zeta}
\end{align}$$
$\displaystyle \bm{\zeta}\in \mathbb{R}^k$是已知常数向量, $\displaystyle \bm{\phi}(\bm{x})$是一个任意向量函数,即要求满足于分布矩与指定函数经验矩相匹配的约束条件,那么最大熵原理 $\displaystyle \textit{maxent} $告诉我们应该选择最大熵分布(最接近于均匀分布的那个)。有约束条件的熵最大化
$$\begin{align}
J(p)=& \mathrm{H}[p]=-\int p (\bm{x})\ln p(\bm{x}) d \bm{x}\\\\
&\mathrm{s.t.}
\begin{cases}
\displaystyle p(\bm{x})\geqslant 0\\\\
\displaystyle \int p(\bm{x})d \bm{x}= 1\\\\
\displaystyle \int \bm{\phi}(\bm{x})p(\bm{x})d \bm{x}=\bm{\zeta}
\end{cases}
\end{align}$$
我们需要使用拉格朗日乘数法,那么拉格朗日算符更新为:
$$\begin{align}
F(p)=-p (\bm{x})\ln p(\bm{x})+\lambda p(\bm{x})+\bm{\eta}^\text{T}\big[\bm{\phi}(\bm{x})p(\bm{x})\big]\\\\
\end{align}$$
我们可以用变分法计算函数 $\displaystyle p$,欧拉-拉格朗日方程是:
$$\begin{align}
-1-\ln p(\bm{x})+\lambda+\bm{\eta}^\text{T}\bm{\phi}(\bm{x})=0\iff p(\bm{x})=\exp[\lambda-1]\exp \big[\bm{\eta}^\text{T}\bm{\phi}(\bm{x})\big]
\end{align}$$
亦有 $\displaystyle p(\bm{x})\propto\exp \big[\bm{\eta}^\text{T}\bm{\phi}(\bm{x})\big]$、给出了归一化常数 $\displaystyle Z=\int \exp \big[\bm{\eta}^\text{T}\bm{\phi}(\bm{x})\big]d \bm{x}$ 有:
$$\begin{align}
p(\bm{x})=\frac{1}{Z}\exp \big[\bm{\eta}^\text{T}\bm{\phi}(\bm{x})\big]
\end{align}$$
因此,最大熵分布 $\displaystyle p(x)$具有指数族的形式,也称为吉布斯分布 $\displaystyle \textit{(Gibbs Distribution)} $。当然我们也可以写成离散形式,这是很容易的,略。
三、广义线性模型$\displaystyle \textit{(GLMs)} $
3.1、概要
我们熟悉了一下指数族,建立广义模型的初衷是要解决,经典线性模型
$$\begin{align}
y=\bm{w}^\text{T}\bm{x}+e\sim\mathcal{N}(\mu,\sigma^2)
\end{align}$$的缺点:
1、因变量 $\displaystyle y$是连续的且服从高斯分布。
2、方差是固定的。
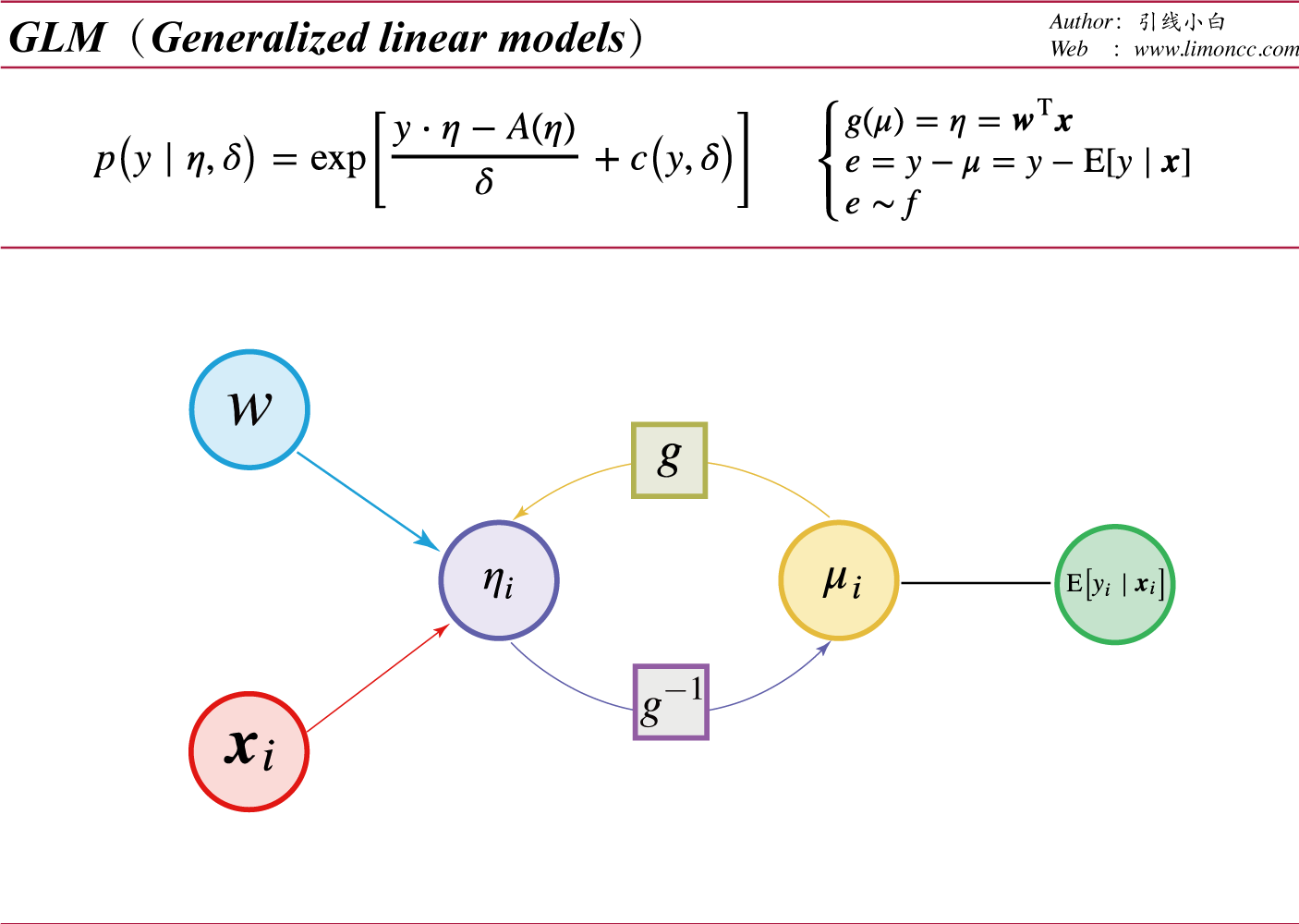
广义线性模型
于是内尔得和韦德伯恩(Nelder & Wedderburn,1972)提出了广义线性模型。我们对指数族的形式稍加修改。
$$\begin{align}
p\left(y\mid\eta,\delta\right)=\exp\left[\frac{y \cdot\eta-A(\eta)}{\delta}+c\left(y,\delta\right)\right]
\end{align}$$
其中 $\displaystyle \delta$是散度参数,通常是1、 $\displaystyle c\left(y,\delta\right)$是归一化参数、 $\displaystyle A(\eta) $ 是分配函数、 $\displaystyle \eta$是连接函数,所谓规范连接函数可以查阅维基百科。同时我们令连接函数:
$\displaystyle g(\mu)=\eta=\bm{w}^\text{T}\bm{x}$
$\displaystyle \mu=\mathrm{E}\left[y\mid \bm{x}\right]=\dot{A}\left(\eta\right)=g^{-1}(\eta)$
$\displaystyle \mathrm{Var}\left[y\right]=\ddot{A}\left(\eta\right)\cdot\delta$
于是有$$\begin{align}
\left\{\begin{matrix}
g(\mu)=\eta=\bm{w}^\text{T}\bm{x}\\\\
e=y-\mu\\\\
e\sim f \end{matrix}\right.
\end{align}$$
再次写出模型:
$$\begin{align}
p \left(y\mid \bm{x} ,\bm{w} ,\delta\right)=\exp\left[\frac{ y\cdot\bm{w}^\text{T}\bm{x}-A(\bm{w}^\text{T}\bm{x})}{\delta}+c\left(y,\delta\right)\right]
\end{align}$$
经过以上分析,可以知道广义线性模型的两个重要不同:
1、连接函数:是因变量 $\displaystyle y$的期望的一个转换,此转换的变量 $\displaystyle g(\mu)$是回归参数 $\displaystyle \bm{w}$的一个线性函数 $\displaystyle \bm{x}^\text{T}\bm{w}$。
2、方差是因变量 $\displaystyle y$期望的函数: $\displaystyle\mathrm{Var}\left[y\right]=\ddot{A}\left(g(\mu)\right)\cdot\delta$
3.2、对数似然函数
广义线性模型有一个很吸引人的特性,即它可与逻辑斯蒂回归使用的方法相同。对于数据集 $\displaystyle \mathcal{D}=\{\bm{x}_i,y_i\}_{i=1}^{n}$我们有对数似然函数:
$$\begin{align}
\ell(\bm{w})
&=\ln p \left(\mathcal{D}\mid \bm{w}\right)
=\frac{1}{\delta}\left[\bm{y}^\text{T}\bm{X}\bm{w}-\sum_{i-1}^{n}A(\bm{w}^\text{T}\bm{x}_i)\right]+\sum_{i=1}^{n}c\left(y_i,\delta\right)\\\\
&=\frac{1}{\delta}\left[\bm{y}^\text{T}\bm{\eta}-\bm{I}^\text{T}A(\bm{\eta})\right]+\bm{I}^\text{T}c\left(\bm{y},\delta\right)
\end{align}$$
有梯度:
$$\begin{align}
&\nabla\ell=\frac{\partial{\ell}}{\partial{\bm{w}}}
=\frac{1}{\delta}\left[\bm{X}^\text{T}\bm{y}-\sum_{i=1}^{n}A’\cdot \bm{x}_i\right]
=\frac{1}{\delta}\left[\bm{X}^\text{T}\bm{y}-\bm{X}^\text{T}\bm{\mu} \right]
=\frac{1}{\delta}\bm{X}^\text{T}\left[\bm{y}-\bm{\mu} \right]
\end{align}$$
有海赛矩阵:
$$\begin{align}
&\bm{H}\left(\ell\right)
=\frac{\partial^2{\ell}}{\partial{\bm{w}\partial\bm{w}^\text{T}}}
=-\frac{1}{\delta}\bm{X}^\text{T}\frac{\partial{\bm{\mu}}}{\partial{\bm{\eta}^\text{T}}}\frac{\partial{\bm{\eta}}}{\partial{\bm{w}^\text{T}}}
=-\frac{1}{\delta}\bm{X}^\text{T}\bm{S}\bm{X}\\\\
\end{align}$$
其中:
$\displaystyle \bm{S}=\frac{\partial{\bm{\mu}}}{\partial{\bm{\eta}^\text{T}}}=\mathrm{diag}\left[\frac{\partial \mu_i}{\partial\eta_i}\right]=\mathrm{diag}\left[\frac{\partial g^{-1}(\eta_i)}{\partial\eta_i}\right]$
$\displaystyle \frac{\partial{\bm{\eta}}}{\partial{\bm{w}^\text{T}}}=\frac{\partial \bm{X}\bm{w}}{\partial\bm{w}^\text{T}}=\bm{X} $
3.3、牛顿-拉弗迭代法。
为了求解模型,现在我们开考虑一下求极值问题,我们要求这样一个数量函数的极值:
$$\begin{align}
\max_{\bm{x}} f\left(\bm{x}\right)
\end{align}$$
我们有梯度: $\displaystyle \nabla f=\frac{\partial f}{\partial\bm{x}}=0$ 同时有海赛矩阵 $\displaystyle \bm{H}\left(f\right)=\frac{\partial f}{\partial\bm{x}\bm{x}^\text{T}}$。
于是我们有梯度的泰勒展开:
$$\begin{align}
\nabla\left(\bm{x}_t\right)=\nabla\left(\bm{x}_t\right)+\bm{H}\left(\bm{x}_t\right)\left[\bm{x}_{t+1}-\bm{x}_t\right]+\bm{r}\left(\bm{x}_t\right)=0
\end{align}$$
忽略余项,可以求得: $\displaystyle \bm{x}_{t+1}=\bm{x}_{t}-\bm{H}^{-1}\left(\bm{x}_t\right)\nabla \left(\bm{x}_t\right)$简写为:
$$\begin{align}
\bm{x}:=\bm{x}-\bm{H}^{-1}\nabla
\end{align}$$
$\displaystyle \\\\$
3.4、极大似然分析
$$\begin{align}
\bm{w}_{t+1}
&=\bm{w}_t -\left[\bm{X}^\text{T}\bm{S}_t\bm{X}\right]^{-1}\bm{X}^\text{T}\left[\bm{y}-\bm{\mu}_t\right]\\\\
&=\left[\bm{X}^\text{T}\bm{S}_t\bm{X}\right]^{-1}\left[\bm{X}^\text{T}\bm{S}_t\bm{X}\bm{w}_t-\bm{X}^\text{T}\left[\bm{y}-\bm{\mu}_t\right]\right]\\\\
&=\left[\bm{X}^\text{T}\bm{S}_t\bm{X}\right]^{-1}\bm{X}^\text{T}\bm{S}_t\left[\bm{\eta}_t-\bm{S}_t^{-1}\left[\bm{y}-\bm{\mu}_t\right]\right]\\\\
&=\left[\bm{X}^\text{T}\bm{S}_t\bm{X}\right]^{-1}\bm{X}^\text{T}\bm{S}_t\bm{\zeta}_t
\end{align}$$
其中:
$\displaystyle \bm{\eta}_t=\bm{X}\bm{w}_t$
$\displaystyle \bm{\mu}_t=g^{-1}\left(\bm{\eta}_t\right)$
$\displaystyle \bm{S}_t
=\frac{\partial\bm{\mu}_t}{\partial\bm{\eta}_t^\text{T}}
=\mathrm{diag}\left[\frac{\partial g^{-1}(\eta_i^t)}{\partial\eta_i^t}\right]$
$\displaystyle \bm{\zeta}_t=\bm{\eta}_t-\bm{S}_t^{-1}\left[\bm{y}-\bm{\mu}_t\right]$
现在我们加以总结,历史上我们称这种算法为:迭代加权最小二乘法(IRLS)
算法:迭代加权最小二乘法(Iteratively reweighted least squares)
1 $\displaystyle \bm{w}_0=g(\bar{y})$
2 $\displaystyle \text{while }\bm{w}=\text{converged}$ :
$\displaystyle
\quad\begin{array}{|lc}
\bm{\eta}_t=\bm{X}\bm{w}_t\\\\\displaystyle
\bm{\mu}_t=g^{-1}\left(\bm{\eta}_t\right)\\\\\displaystyle
\bm{S}_t=\frac{\partial\bm{\mu}_t}{\partial\bm{\eta}_t^\text{T}}\\\\\displaystyle
\bm{\zeta}_t=\bm{\eta}_t-\bm{S}_t^{-1}\left[\bm{y}-\bm{\mu}_t\right]\\\\\displaystyle
\bm{w}_{t+1}=\left[\bm{X}^\text{T}\bm{S}_t\bm{X}\right]^{-1}\bm{X}^\text{T}\bm{S}_t\bm{\zeta}_t
\end{array}\\\\
$
3 #end while
如果我们扩展这个推导来处理非规范连接函数,我们就会发现海赛矩阵有另一个术语。然而结果表明海赛矩阵期望与公式相同;使用海赛矩阵期望(称为 $\displaystyle \textit{Fisher} $信息矩阵)来替代实际的海赛矩阵,称为 $\displaystyle \textit{Fisher}$评分方法。
在此基础上,我们可以简单地将上述过程修改为高斯先验的 $\displaystyle \textit{MAP} $估计,即我们只需修改目标、梯度和海赛矩阵,就像我们对逻辑斯蒂回归增加 $\displaystyle \ell_2$正则一样。
4、评述
使用广义线性模型我们解决了指数族分布的通用贝叶斯模型。这里我们跳过了多元高斯分布的模型。这涉及到高维,和多元统计的wishart分布。需要更为高级的工具:
1、格拉斯曼代数
2、微分形式
3、外微分
稍后,我们将一一提及它们。继续我们的星辰大海。
| 版权声明 |  |
| 由引线小白创作并维护的柠檬CC博客采用署名-非商业-禁止演绎4.0国际许可证。 本文首发于柠檬CC [ https://www.limoncc.com ] , 版权所有、侵权必究。 | |
| 本文永久链接 | httpss://www.limoncc.com/post/c7d551950374c4114400ca0e635169ba/ |
| 如果您需要引用本文,请参考: |
| 引线小白. (Mar. 9, 2017). 《广义线性模型》[Blog post]. Retrieved from https://www.limoncc.com/post/c7d551950374c4114400ca0e635169ba |
| @online{limoncc-c7d551950374c4114400ca0e635169ba, title={广义线性模型}, author={引线小白}, year={2017}, month={Mar}, date={9}, url={\url{https://www.limoncc.com/post/c7d551950374c4114400ca0e635169ba}}, } |