作者: 引线小白-本文永久链接:httpss://www.limoncc.com/post/d9321405ef13c11b/
知识共享许可协议: 本博客采用署名-非商业-禁止演绎4.0国际许可证
[TOC]
一、前言
最近一种称为Bone微调[^1]的技术比起LoRA微调表现的又快又好。下面我们来深入认识一下,这个技术。LoRA诞生以来因为节省资源和其效果,受到大家的广泛使用。它的变体致力于改善与全参数微调差距,有OLoRA、LoRA-Ga等。对这种低秩微调范式的优化似乎走到了极致。就在上月(2024年11月)出现了一篇与低秩微调范式完全不同的新的高效微调方法。它借鉴了GQA和MQA的思想,拆分权重矩阵为多块,每块共享一个可更新小的权重。称之为block-affine-adaptation:块映射自适应。
Bone微调已在包含在最新的PEFT库中,建议使用配合transformersv4.46.3使用,该版本修正了累计梯度的问题,莫要使用4.47.0,这个版本笔者测试累计梯度存在loss翻倍的问题。
注意本文图中的灰色块表示PAD,即补0。
二、原理
要实现高效的参数微调,必然要减少可微调的参数。那么问题关键就变成了如何缩小?以LoRA为代表的低秩微调范式认为这样操作:
$$\begin{align}
\bm{y} &= \left(\bm{W}_{out\times in}+\Delta \bm{W}\right)\bm{x}_{in}\\
&= \left(\bm{W}_{out\times in}+\bm{B}_{out\times r}\bm{A}_{r\times in }\right)\bm{x}_{in}
\end{align}$$
其中 $r\ll \mathrm{Rank}[\bm{W}]$
Bone借鉴了GQA和MQA的思想,它是这么操作的
$$\begin{align}
\bm{y} &= \left(\bm{W}_{out\times in}+\Delta \bm{W}\right)\bm{x}_{in}\\
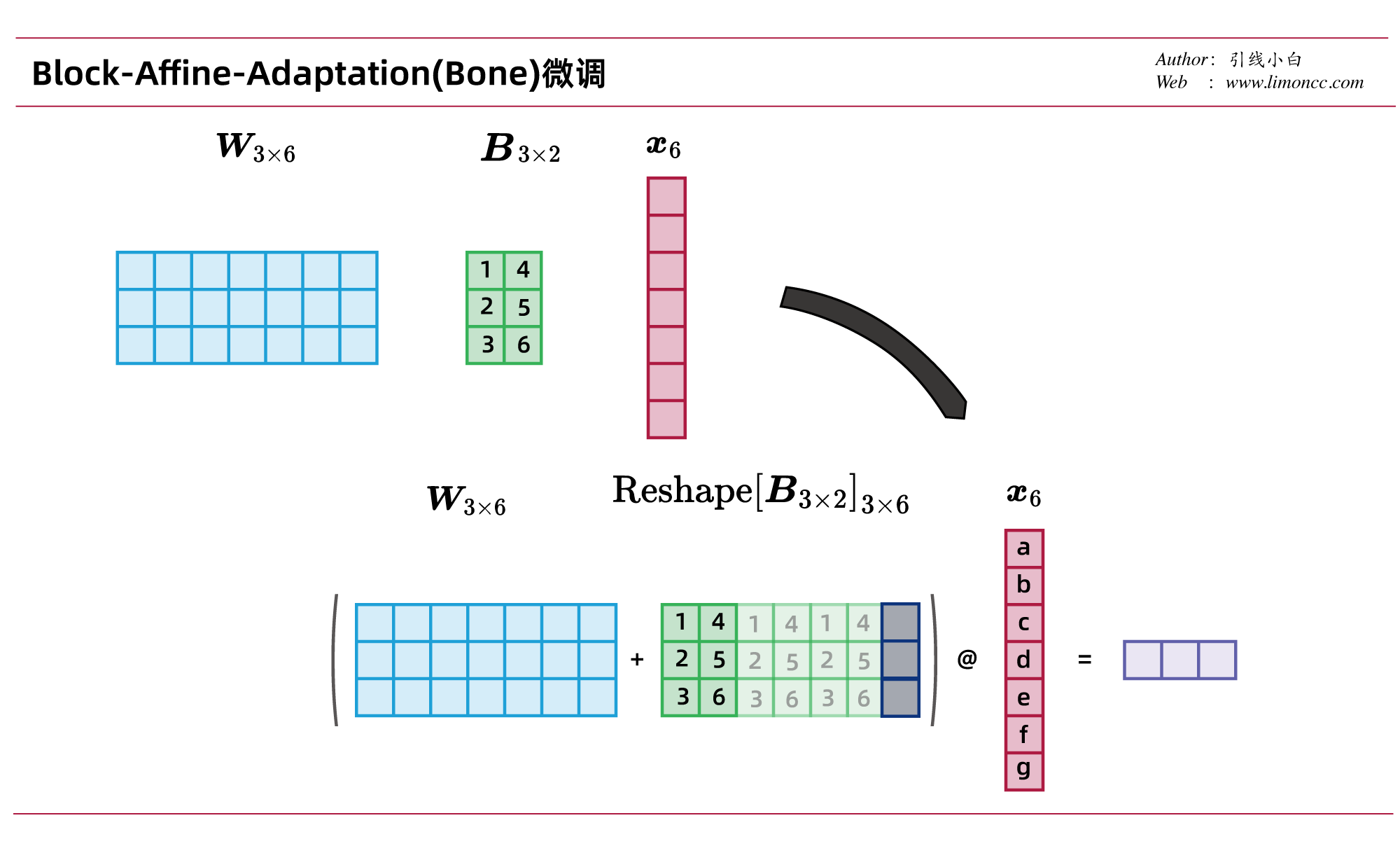
&= \left(\bm{W}_{out\times in}+\mathrm{Reshape}\left[\bm{B}_{out\times r}\right]_{out\times in}\right)\bm{x}_{in}
\end{align}$$
其中 $\displaystyle \mathrm{Reshape}$操作其实就是复制 $\bm{B}_{out\times r}$并根据需要填充 $0$到 $out\times in$维度。且 $r\ll in$。 $in$表示输入维度, $out$表示输出维度。
本文中的公式与Bone论文中的公式略有不同,说实话论文中的公式和做图有点过于简约了。
三、小试牛刀
Bone微调方法,思想其实非常简单:实质就是矩阵分块共享更新到权重。它的效果如何呢,原论文的实验结果是收敛更快,loss更低。笔者在qwen2.5-0.5b上进行大家喜闻乐见的自我认知微调。效果如下:
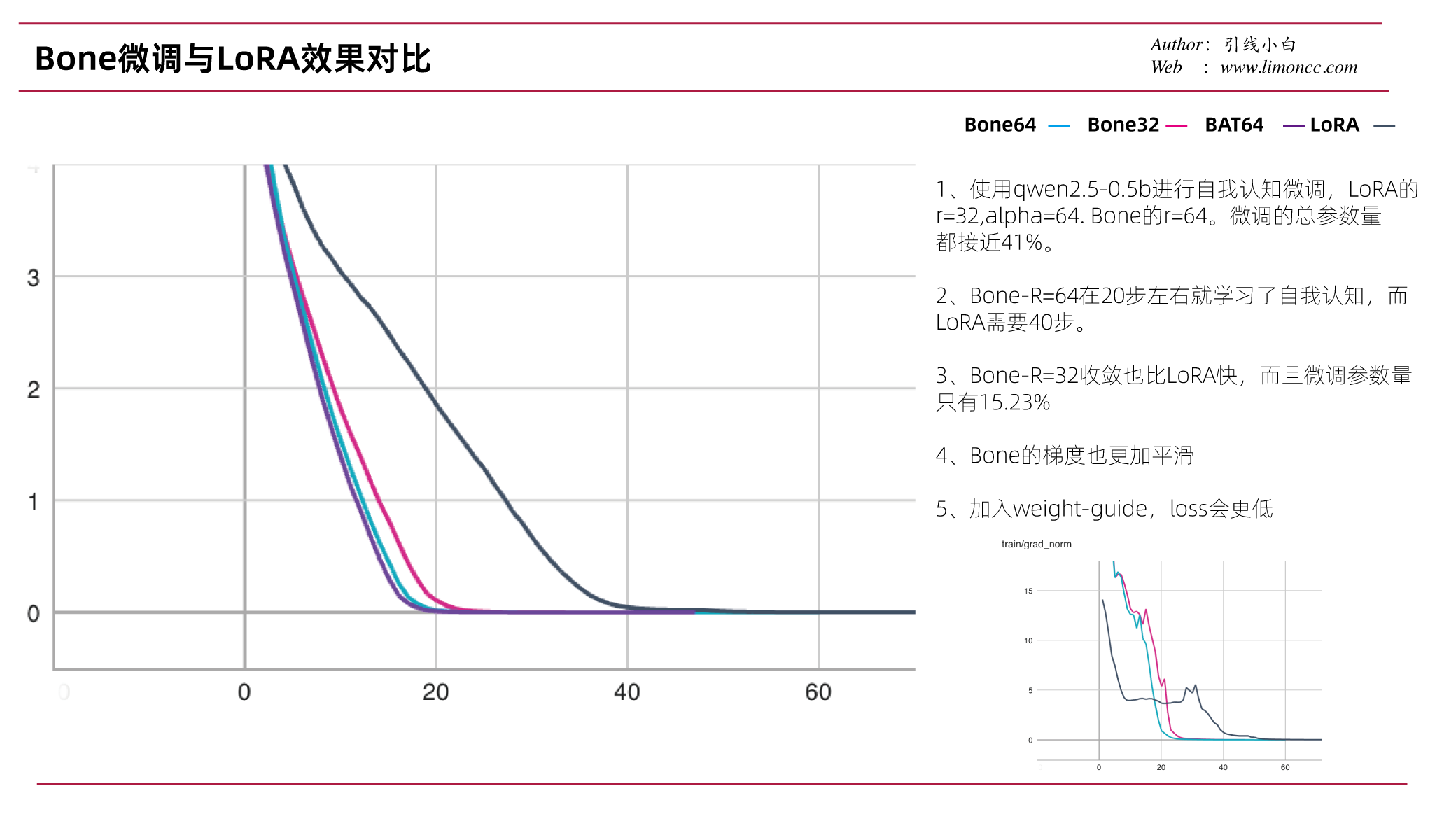
确实如论文所说收敛更快,loss更低。需要微调的参数量也更小。
四、具体实现
4.1、Bone
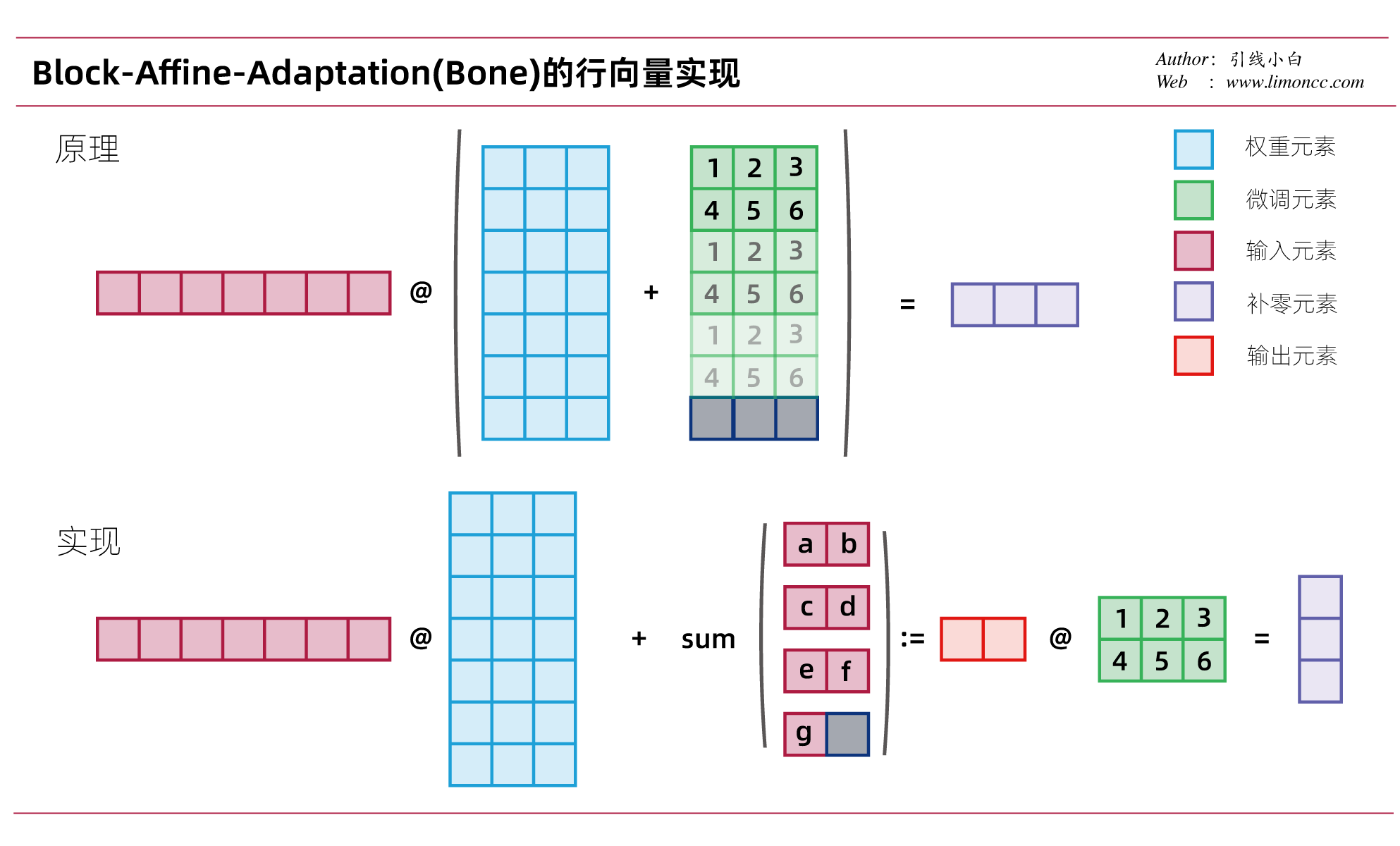
数学上我们的一般用列向量,而在机器学习中我们常用行向量。下面我们来探究一下Bone(block-affine-adaptation)的具体实现:调整输入 $x$的形状后求和,而不是拼接 $\bm{B}$矩阵。能实现同样目的,也更加节省内存。具体来说就是
$$\begin{align}
\bm{y} &= \bm{x}_{in}^\T\left[\bm{W}_{in\times out}+\Delta \bm{W}\right]\\
&= \bm{x}_{in}^\T\bm{W}_{in\times out}+\mathrm{sum}\left[\mathrm{Reshape}\left[\bm{x}_{in}\right]_{[\frac{in}{r}],r},dim=-2\right]\bm{B}_{r\times out}
\end{align}$$
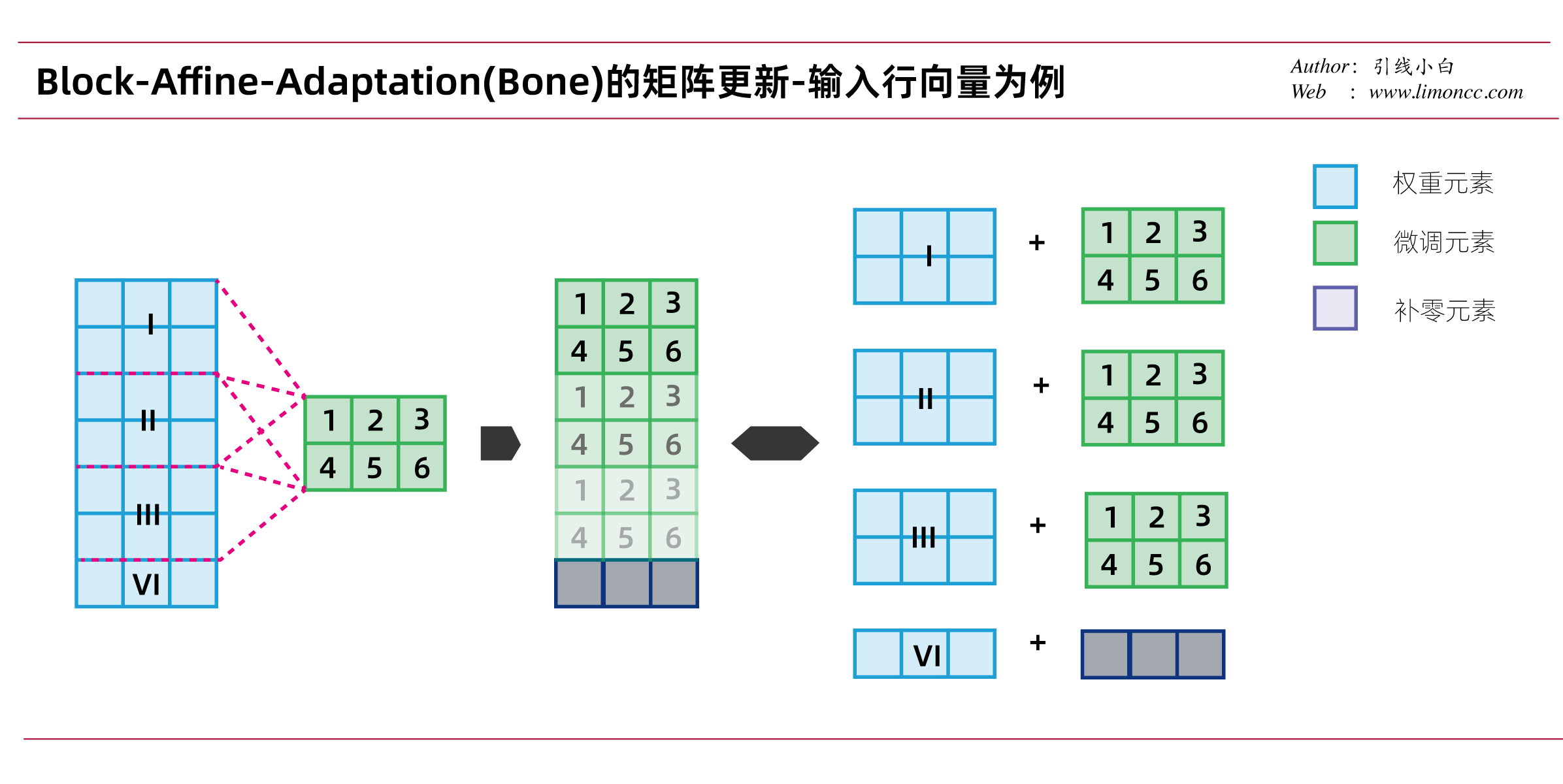
再来一个图,Bone微调的矩阵是如何更新的:
接下来就是代码实现了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34import torch
import random
import numpy as np
from einops import rearrange
import torch.nn.functional as F
# 固定种子
seed = 12
torch.manual_seed(seed)
if torch.mps.is_available():
torch.mps.manual_seed(seed)
elif torch.cuda.is_available():
torch.cuda.manual_seed(seed)
random.seed(seed)
np.random.seed(seed)
# 权重矩阵in_feature x out_feature = 7 x 3
w = torch.randn(7,3)
# 微调矩阵rank x out_feature = 2 x 3
delta_w = torch.randn(2,3)
# bone的矩阵更新 rank=2
r = 2
# 输入x的维度是 batch x in_feature =1 x 7
x = torch.randn(1,7)
# 计算需要补全的大小
padding_size = (r - x.size(-1) % r) % r
# 对x补全
x_padded = F.pad(x, (0, padding_size))
# 对x塑形
x_reshaped = rearrange(x_padded, '... (d r) -> ... d r', r=r)
# 计算输出
y = x@w + torch.sum(x_reshaped, dim=-2)@delta_w
print(y.numpy())
# dim(y) = batch x out_feature
# [[-0.5105, 4.1959, -0.2296]]
最后贴一下PEFT的源代码实现1
2
3
4
5
6
7
8
9
10
11# peft/tuners/bone/layer.py 323-332
result = self.base_layer(x, *args, **kwargs)
for active_adapter in self.active_adapters:
if active_adapter not in self.bone_block.keys():
continue
bone = self.bone_block[active_adapter]
r = bone.size(0)
if x.size(-1) % r != 0:
padding_size = (r - x.size(-1) % r) % r
x = F.pad(x, (0, padding_size))
result = result + torch.sum(x.reshape(*x.shape[:-1], x.size(-1) // r, r), dim=-2) @ bone
也不补充一下列向量实现
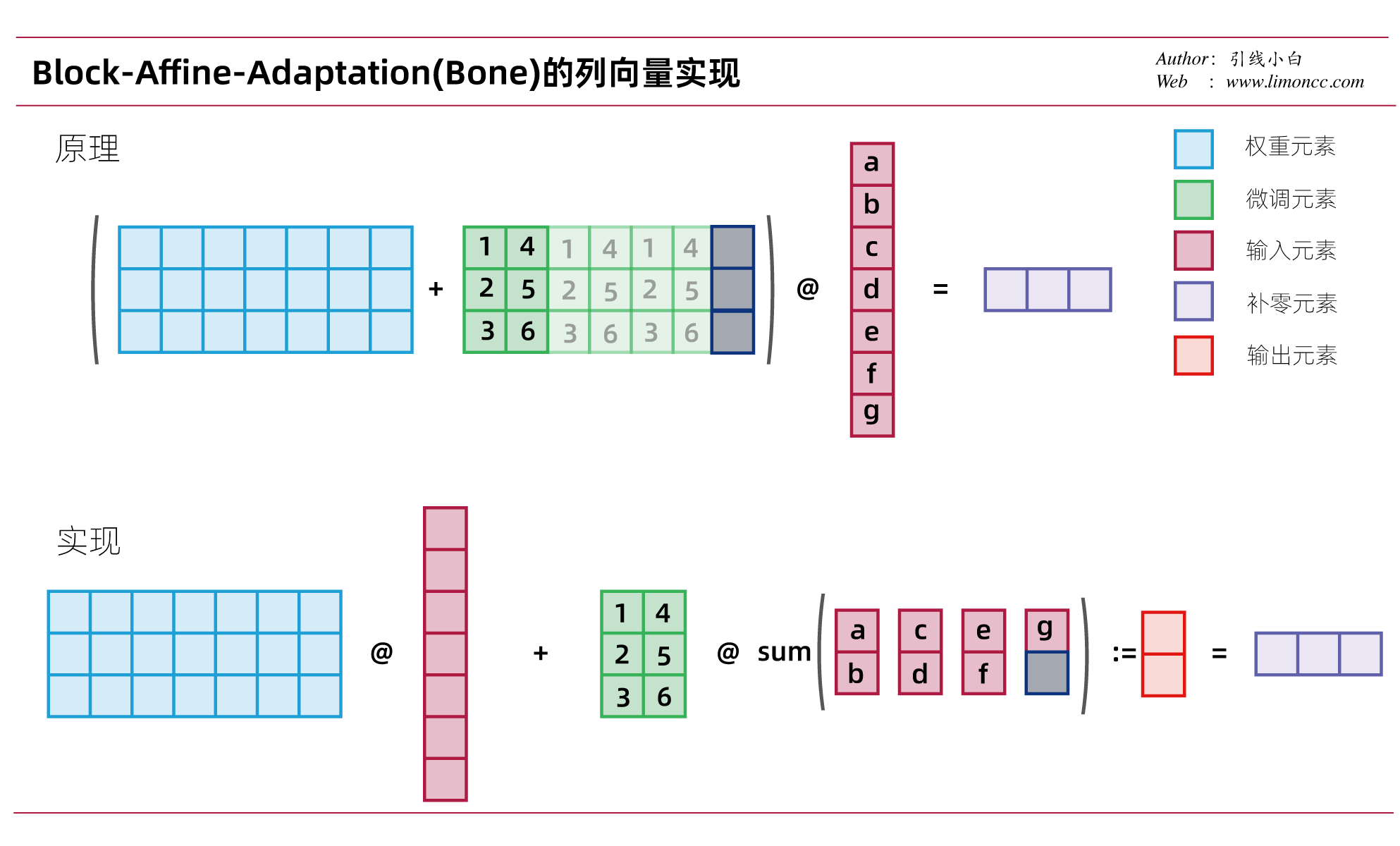
4.2、BAT
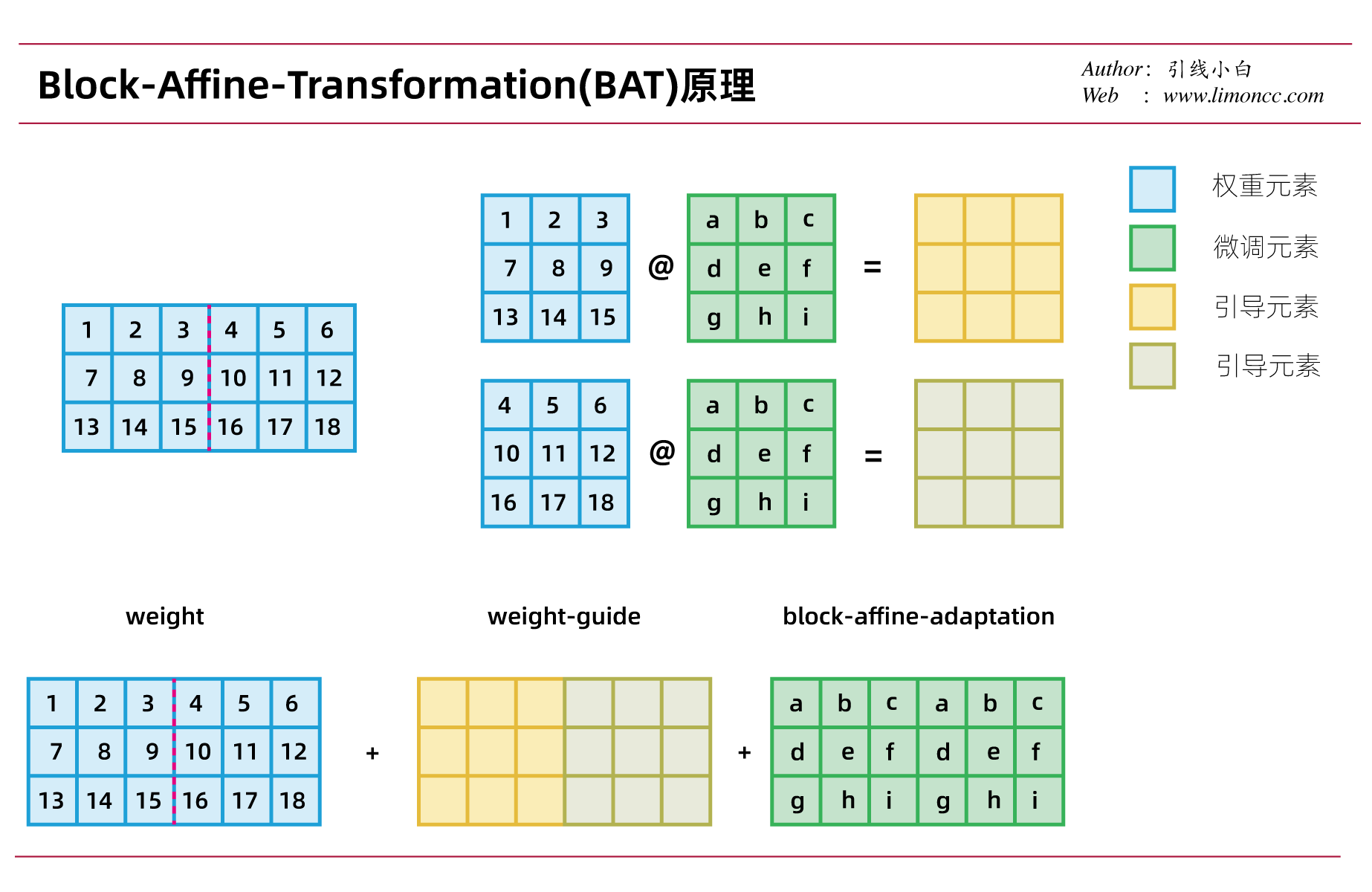
我们可以看到Bone微调的分块矩阵是共享同一个微调矩阵。然而按理说分块矩阵应该是不同的,它们的梯度信息应该不是一样的,而且也没有利用到分块矩阵矩阵的信息。这启发我们设法利用分块矩阵,而这就是论文中中提出的Block-Affine-Transformation(BAT)。它的原理如下:
$$\begin{align}
\bm{W}_{in/r\times out/r\times r\times r}&=\mathrm{Reshape}\left[\bm{W}_{out\times in}\right]\\
\bm{B}_{out/r\times r \times r}&=\mathrm{Reshape}\left[\bm{B}_{r\times out}\right]\\
\Delta \bm{W}_{in \times out}&=\mathrm{Reshape}\left[\bm{W}_{in/r\times out/r\times r\times r}\odot\bm{B}_{out/r\times r \times r}+\bm{B}_{out/r\times r \times r}\right]
\end{align}$$
看公式有点不清不楚,实际就是每个分块矩阵与微调矩阵做乘法形成所谓的weight-guide矩阵,这个矩阵包含的分块矩阵中的信息,从而期望来引导微调矩阵针对每个分块矩阵做更新。
下面给出了一个例子:
$$\begin{align}
\bm{W}_{weight-guide} = \mathrm{Reshape}\left[\bm{W}_{in/r\times out/r\times r\times r}\odot\bm{B}_{out/r\times r \times r}\right]
\end{align}$$
其中 $\odot$表示哈达玛积(Hadamard product),即matlab里面说的点乘运算。Reshape操作不过是实现每个分块矩阵与微调矩阵做乘法而做的矩阵塑形。
BAT微调有一个潜在要求rank必须是in_feature和out_feature的维度的公倍数。
1 | # 权重矩阵in_feature x out_feature = 6 x 3 |
PEFT的代码实现1
2
3
4
5# peft/tuners/bone/layer.py 225-230
w = (orig_weight.reshape(orig_weight.size(0) // r, r, orig_weight.size(1) // r, r).permute(2, 0, 1, 3)
+ weight_bone)
output_tensor = w.permute(1, 2, 0, 3).reshape(*orig_weight.shape)
[^1]: Kang, J. (2024, November 28). Bone: Block-Affine Adaptation of Large Language Models. arXiv. https://doi.org/10.48550/arXiv.2409.15371
| 版权声明 |  |
| 由引线小白创作并维护的柠檬CC博客采用署名-非商业-禁止演绎4.0国际许可证。 本文首发于柠檬CC [ https://www.limoncc.com ] , 版权所有、侵权必究。 | |
| 本文永久链接 | httpss://www.limoncc.com/post/d9321405ef13c11b/ |
| 如果您需要引用本文,请参考: |
| 引线小白. (Dec. 12, 2024). 《Bone微调,超越LoRA系列的高效微调方法——大语言模型研究04》[Blog post]. Retrieved from https://www.limoncc.com/post/d9321405ef13c11b |
| @online{limoncc-d9321405ef13c11b, title={Bone微调,超越LoRA系列的高效微调方法——大语言模型研究04}, author={引线小白}, year={2024}, month={Dec}, date={12}, url={\url{https://www.limoncc.com/post/d9321405ef13c11b}}, } |